Глава 11. Метод валентных связей и его применение к двухатомным молекулам

11.1. Молекула водорода

Первое успешное объяснение химической связи было опубликовано в 1927 г. Гайтлером и Лондоном; эта работа легла в основу так называемого метода валентных связей (ВС). Наиболее существенным в этом методе является предположение, что при образовании молекулы в основном сохраняется электронная структура составляющих ее атомов и энергия ковалентной связи обусловлена обменом электронов между атомами. Сначала рассмотрим метод Гайтлера - Лондона для молекулы водорода.

Атом водорода в основном состоянии содержит один электрон на 1s-орбитали. Обозначим ядро атома буквой а, электрон - цифрой 1 и волновую функцию - 1s_a (1). Второй атом (с ядром b и электроном 2) описывается волновой функцией 1s_b (2). Если атомы расположены далеко один от другого, то волновая функция всей двухатомной системы есть

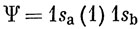
Гамильтониан системы имеет вид

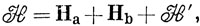
где Н_а и Н_b - гамильтонианы атомов, и

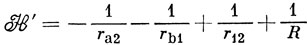
можно рассматривать как члены гамильтониана, выражающие взаимодействие между атомами. Энергия, вычисленная с функцией (11.1), равна

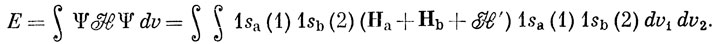
Пользуясь тем, что 1s_a и 1s_b - собственные функции гамильтонианов Н_а и H_b соответственно [см. уравнение (10.18)], получаем

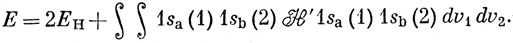
Входящий в уравнение (11.5) интеграл, обозначенный далее через Q, разбивается на части в соответствии с уравнением (11.3) и после интегрирования по координатам запишется в виде

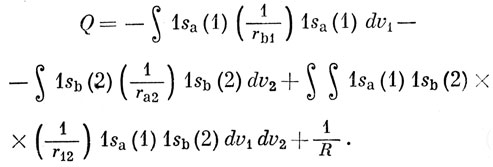
Первое слагаемое представляет энергию притяжения электронного заряда с плотностью 1s_a², к ядру b, второе - притяжение электронного заряда с плотностью 1s_b² к ядру а, третье - отталкивание электронных зарядов с плотностями 1s_а² и 1s_b² и, наконец, последнее слагаемое есть энергия отталкивания ядер. Таким образом, Q представляет собой просто классическую электростатическую энергию взаимодействия двух атомов водорода, и поэтому Q называют кулоновским интегралом. Вычисление этого интеграла дает пренебрежимо малое значение энергии связи, составляющее лишь 5% от наблюдаемой величины. Волновая функция (11.1) является слишком грубой для молекулы водорода, так как она соответствует состоянию, в котором каждый электрон локализован около одного из ядер. С равным основанием можно взять функцию 1s_a (2) 1s_b (1). Правильная волновая функция молекулы Н₂ должна давать одинаковую вероятность нахождения каждого электрона как около одного, так и около другого ядра. Этому условию удовлетворяют функции

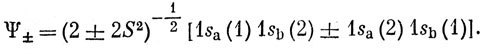
Здесь множитель перед квадратной скобкой обеспечивает нормировку, причем

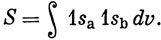
Вычисляя энергию с функциями (11.7) таким же способом, как и ранее, получим

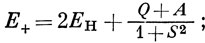
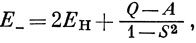
где Q определено, а А - так называемый обменный интеграл ^*):

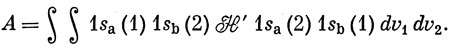
^*) (К сожалению, термины "кулоновский интеграл" и "обменный интеграл" употребляются в методах МО и ВС в различных смыслах [см. уравнение (10.64)].)

Подставляя в уравнение (11.10) H' в явном виде, находим

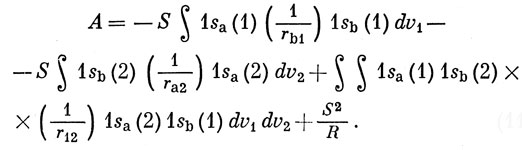
Первые два интеграла уже встречались при рассмотрении H₂⁺ методом МО [см. выражение (10.21)]. Третье слагаемое - двухэлектронный обменный интеграл. Вычисления показывают, что сумма первых двух слагаемых по абсолютной величине больше, чем сумма последних двух, т. е., согласно соотношению (11.9), функции ₊ соответствует более низкая энергия, чем функции Ψ_-. Вычисленная с функцией Ψ₊ энергия связи молекулы водорода составляет около 60% от наблюдаемой на опыте величины. Функцию Ψ₊ обычно называют функцией Гайтлера - Лондона.

До сих пор в волновой функции не учитывался спин: Ψ₊ симметрична относительно перестановки электронов, и, согласно принципу Паули, она должна умножаться на антисимметричную спиновую функцию, а это дает синглетное состояние [см. равенство (9.24)]:

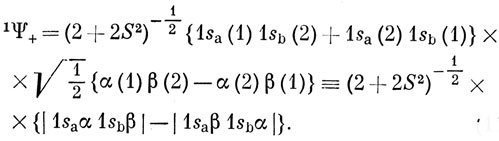
Функцию Ψ_-, которая соответствует отталкиванию атомов водорода, следует умножить на симметричную спиновую функцию, что дает триплетное состояние [см. равенство (9.23)]:

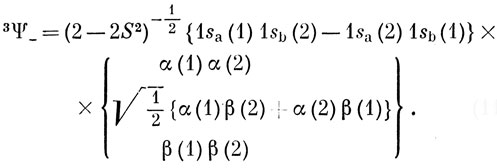
Из соотношения (11.9) следует, что, если оба ядра сливаются, энергия состояния ³Ψ_- стремится к бесконечности, потому что при этом S → 1. Это бесконечное по величине отталкивание можно связать ^*) с нарушением принципа запрета, которое наблюдалось бы для состояния ³Ψ_- при 1s_а = 1s_b.

^*) (Это объяснение неверно. При сближении ядер энергия не только ³Ψ_--, но и ¹Ψ₊-состояний стремится к бесконечности как

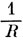
по причине кулоновского отталкивания точечных зарядов ядер. Что же касается ³Ψ_--состояния, то не трудно видеть, что при слиянии ядер формула (11.9) для энергии и выражение (11.7) для волновой функции становятся неопределенными. Раскрытие неопределенностей показывает, что волновая функция ³Ψ_- переходит в функцию ³Р-состояния объединенного атома с электронной конфигурацией 1sσ2pσ, а формула (11.9) при отбрасывании из гамильтониана члена 1/R дает приближенно энергию этого ³Р-состояния атома. - Прим. ред.)

Описание ковалентной связи в методе ВС основано на волновой функции Гайтлера - Лондона (11.12). Если две атомные орбитали φ_а и φ_b перекрываются, на каждой из них находится по одному электрону, и если их спины противоположны, т. е. дают синглетное состояние, то волновая функция вида (11.12)

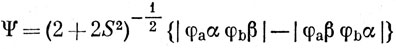
соответствует образованию связи. Если же на одной или обеих атомных орбиталях находится по два электрона, то невозможно написать такую функцию, не нарушая принципа запрета. Далее, если интеграл перекрывания функций φ_а и φ_b равен нулю, например в силу свойств симметрии функций, то в синглетном состоянии не возникает связи, так как первые два члена в выражении (11.11) равны нулю и обменный интеграл становится положительным. В этом случае триплетное состояние обладает более низкой энергией, чем синглетное.