11.2. Гомоядерные двухатомные молекулы

Рассмотрим теперь молекулу азота. Основная конфигурация атома азота есть (1s)² (2s)² (2p)³, основное состояние - ⁴S, и на каждой из трех р-орбиталей находится по одному электрону. Отсюда следует, что каждый из этих трех электронов может образовать связь с соответствующим электроном другого атома: электроны, занимающие p_z-орбитали, образуют σ-связь, а электроны, находящиеся на р_х- и р_y-орбиталях, - две π-связи. Это описание ничуть не хуже того, которое дается методом МО, однако волновая функция, характеризующая эти связи, оказывается довольно сложной.

Волновая функция σ-связи (ось z направлена вдоль линии связи) имеет вид ^*)

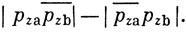
^*) (Здесь используется обозначение, введенное на стр. 114 для различения спиновых состояний.)

Для π_x- и π_y-связей функции записываются соответственно как

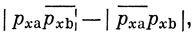
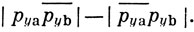
Волновую функцию молекулы в целом (не принимая во внимание 1s- и 2s-электроны, которые, как полагают, не участвуют в образовании связи) можно записать тогда следующим образом:

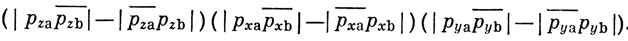
Однако эта функция не учитывает возможности обмена электронов, находящихся, например, на р_z- и р_х-АО. Чтобы учесть такую возможность, приходится записывать волновую функцию с помощью определителей 6-го порядка:

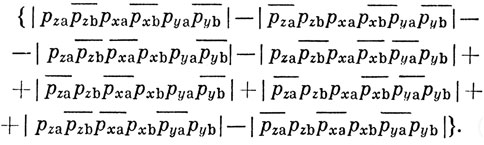
Чтобы построить эту функцию, достаточно перемножить все слагаемые в выражении (11.16), как если бы они не были определителями, а затем полученные произведения записать как определители. Волновая функция (11.17) изменяет знак, если переставить спиновые функции, относящиеся к любой паре орбиталей, образующих связь. Таков общий метод нахождения функции Гайтлера - Лондона. Если она описывает n двухэлектронных связей, то полная запись такой функции содержит 2ⁿ определителей.

Сравним теперь функцию (11.17) с соответствующей волновой функцией молекулы N₂, полученной по методу МО (табл. 10.2):

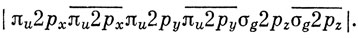
Эту функцию, конечно, проще записать и с нею удобнее оперировать. Однако из этого не следует, что она является лучшей функцией, если таковой считать ту, которая соответствует более низкому значению энергии.

Очевидно, удобно иметь краткое обозначение для функций в методе ВС. Используем символ

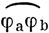
для обозначения связи между орбиталями φ_а и φ_b. Тогда волновая функция (11.17) перепишется в виде

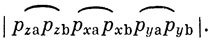
Применим теперь метод ВС к молекуле O₂. Атом кислорода имеет четыре электрона в 2p-оболочке. Это значит, что два из них могут участвовать в образовании связи. Поскольку σ-связь характеризуется более низкой энергией, чем π-связь, следует ожидать, что в молекуле кислорода будет одна σ-связь и одна π-связь. Этому соответствует волновая функция

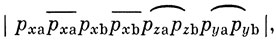
где

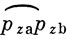
обозначает σ-связь, а

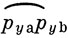
- π-связь. Другие орбитали, относящиеся к π-симметрии (р_ха и р_хb), содержат неподеленные пары электронов.

Функция (11.20) имеет два недостатка. Во-первых, она не может описывать основное состояние молекулы O₂, так как это состояние является триплетным, а функция Гайтлера - Лондона всегда относится к синглетному состоянию. Во-вторых, функция (11.20) не относится ни к ∑-, ни к Δ-состояниям, а отвечает смеси этих состояний.

В методе ВС, как мы уже видели, триплетная функция является разрыхляющей, если две образующие ее орбитали перекрываются друг с другом, и связывающей, если они взаимно ортогональны. Это наводит на мысль, что π-связь в молекуле O₂ следует рассматривать как образованную двумя электронами, находящимися на взаимно ортогональных орбиталях, спины которых дают триплетное состояние.

Если исходить из волновой функции, построенной по методу МО для π-связей ³∑_g^--состояния молекулы O₂ (например, соответствующей M_s = 1), то, переходя к π-орбиталям, записанным в комплексной форме (π⁺ и π^-) ^*), имеем

^*) (

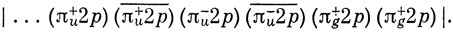
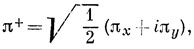
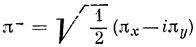
(см. в гл. 3 действительную и комплексную формы р-орбиталей).)

Если затем представить МО в виде линейной комбинации соответствующих атомных орбиталей,

то члены в волновой функции, которые соответствуют одинаковому числу электронов на атомах а и b, имеют вид

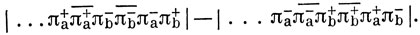
Каждому определителю соответствует электронная пара на атоме а, электронная пара на атоме b, а также триплетная двухэлектронная связь между π⁺-орбиталью одного из атомов и π^--орбиталью другого. Кроме этих слагаемых, будут также члены, описывающие ионные структуры молекулы O₂.

По-видимому, нет достаточно удовлетворительного способа изображения связи в молекуле O₂ с помощью химической структурной формулы. Обычную парную связь Гайтлера - Лондона между атомами А и В будем обозначать А - В. В случае триплетного разрыхляющего состояния пары электронов удобно выражать в виде А··В. Триплетная связывающая пара электронов встречается очень редко, но для полноты ее можно обозначить А ∼ В.

Как уже указывалось на примере молекулы LiH, σМО содержат существенную примесь 2s- и 2рσ-АО. Это имеет место и для гомоядерных двухатомных молекул, хотя степень 2s - 2p-взаимодействия убывает по мере перехода от молекулы Li₂ к молекуле F₂ (стр. 51). В методе ВС 2s - 2р-взаимодействие вводят посредством гибридизации (см. гл. 5). Для иллюстрации этого рассмотрим Li₂. Волновая функция Гайтлера - Лондона в своей простейшей форме (11.14) для одиночной σ-связи в молекуле Li₂ имеет вид

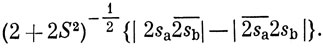
Однако всегда можно улучшить эту функцию, сделав ее более "гибкой" и применив вариационный принцип. В частности, энергию, вычисленную с функцией

где

можно минимизировать относительно параметра λ.

При увеличении λ от нуля растет перекрывание атомных орбиталей φ_а и φ_b. Это показано на рис. 11.1. Для 2s- и 2pσ-орбиталей атома Li приняты слэтеровские функции (гл. 4), а интегралы перекрывания вычислены при равновесной длине связи 2,67 А. Из рис. 11.1 видно, что имеется максимум при λ = 0,7, и этот максимум имеет неожиданно большое значение 0,95 (хотя, если для 2s-орбитали вместо слэтеровской функции использовать радиальную функцию с узлом, интеграл перекрывания несколько уменьшится).

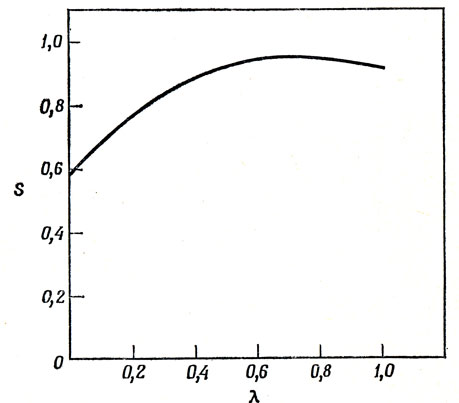
Рис. 11.1. Влияние sр-гибридизации на величину интеграла перекрывания между двумя σ-орбиталями атома Li в молекуле Li₂

Энергия, вычисленная с функцией (11.25), понижается при увеличении интеграла перекрывания функций φ_а и φ_b и в то же время возрастает при увеличении доли 2рσ-функции в гибридной орбитали (так как энергия 2р-орбитали на 1,85 эв выше энергии 2s-орбитали). Лучшая волновая функция соответствует, таким образом, некоторому компромиссу между этими двумя эффектами, со значением λ, вероятно, находящимся в интервале от 0,2 до 0,4.