Глава 12. Химическая связь в многоатомных молекулах

12.1. Сравнение методов МО и ВС для двухатомных молекул

В начале этой главы сравниваются методы МО и ВС в их простейшей форме для молекулы водорода, чтобы показать их ограниченность и выяснить, какие улучшения могут быть сделаны для построения более точных волновых функций.

В методе МО волновая функция молекулы Н₂ получается, если два электрона с противоположными спинами поместить на орбиталь σ_g1s = N (1s_a + 1s_b).

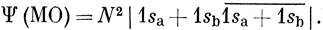
Этот определитель можно представить в виде

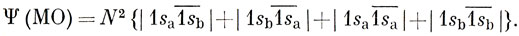
Первые два слагаемых представляют собой функцию Гайтлера - Лондона (11.12) для молекулы Н₂, а два других соответствуют ионным структурам Н^-Н⁺ и Н⁺Н^-. Можно сказать, что волновая функция, построенная по методу МО, равна сумме ковалентной и ионной функций:

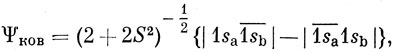
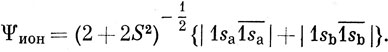
С другой стороны, простой метод ВС для молекулы Н2 основан лишь на одной ковалентной функции. Какое же из этих двух описаний ближе к истине?

Ясно, что функция, построенная по методу МО, при больших межъядерных расстояниях является довольно грубой. Она соответствует диссоциации молекулы Н₂ на смесь ионов и атомов (в одинаковых количествах), в то время как на самом деле продуктами диссоциации основного состояния молекулы Н₂ являются нейтральные атомы. С другой стороны, при очень малых расстояниях между ядрами следует ожидать, что вероятность нахождения обоих электронов как на одной и той же АО, так и на различных орбиталях одинакова. Этот вывод согласуется с описанием молекулы Н₂ по методу МО.

Расчет энергии диссоциации молекулы Н₂ с функцией Гайтлера - Лондона дает 3,14 эв при равновесном расстоянии между ядрами, равном 0,87 А. Расчет по методу МО приводит к значительно худшему результату для энергии диссоциации (2,65 эв), но к несколько лучшему значению равновесного межъядерного расстояния (0,85 А). Однако оба результата так далеки от экспериментальных значений (4,75 эв; 0,74 А), что трудно дать предпочтение одной из этих функций. Лучшее приближение, чем оба упомянутых, можно получить, если варьировать параметр, характеризующий отношение весов ионной и ковалентной структур:

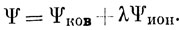
Используя вариационный принцип, можно получить для параметра λ величину 0,16, если ковалентная и ионная функции построены из водородных орбиталей. Все же полученную функцию вряд ли можно считать существенно улучшенной по сравнению с функцией Гайтлера - Лондона, так как при расчете с ней для энергии диссоциации получается 3,23 эв, а для равновесного расстояния - 0,88 А. Однако если варьировать также и показатель экспоненты атомной 1s-функции, то при ζ_ион = ζ_ков = 1,193 и λ = 0,25 получается весьма значительное улучшение результатов расчета (4,02 эв; 0,75 А) по сравнению как с одной лишь ковалентной функцией, так и с наилучшей функцией, построенной по методу МО. Эти результаты собраны в табл. 12.1.

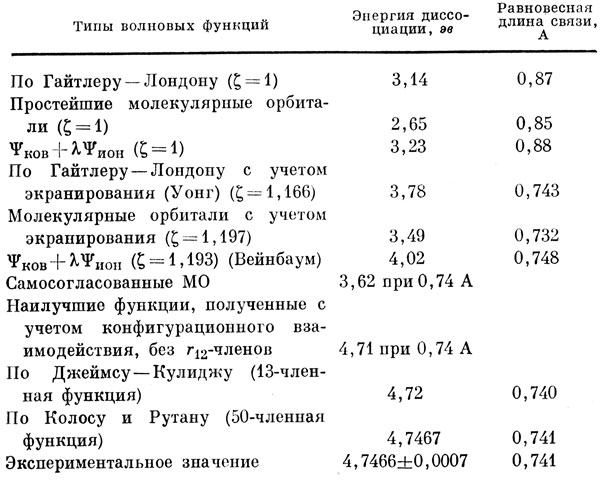
Таблица 12.1. Расчеты молекулы Н₂

Резонансу ионной и ковалентной структур в методе ВС соответствует так называемое конфигурационное взаимодействие в методе МО. Это понятие означает, что волновая функция берется в виде линейной комбинации функций, отнесенных к различным электронным конфигурациям. Например, дважды возбужденная конфигурация которая образуется двумя электронами молекулы Н₂ на разрыхляющей σ_u1s-орбитали, обладает также симметрией ¹∑_g^+*). Тогда улучшенная по сравнению с простейшей формой метода МО волновая функция получается наложением двух ¹∑_g⁺-функций, одна из которых соответствует основному состоянию (σ_g1s)², а другая - дважды возбужденному (σ_u1s)²:

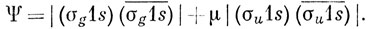
^*) (Конфигурация (σ_g1s)(σ_u1s) приводит к состояниям, которые не вносят вклада в волновую функцию основною состояния, так как обладают другой симметрией.)

Можно показать, что эта волновая функция с точностью до нормировочной постоянной совпадает с функцией (12.4), если

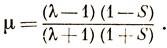
Поскольку λ и μ определяются вариационным методом, то функции (12.4) и (12.5) должны быть идентичными.

Волновая функция, построенная для молекулы Н₂ по методу МО, не учитывает корреляцию электронов (см. стр. 177). Из ее вида следует, что если один электрон находится на 1s_а-орбитали, то другой может находиться как на 1s_a-, так и на 1s_b-орбитали. С другой стороны, функция, построенная по методу ВС, переоценивает роль корреляции электронов [пользуясь выражениями (11.27) и (11.28), можно проверить, что для этой функции Р (1, 2) ≠ Р (1) Р (2)]: если один электрон находится на 1s_a-орбитали, то другой должен быть на орбитали 1s_b. Правильный учет корреляции находится где-то посередине между этими двумя крайними случаями, но несколько ближе к случаю Гайтлера - Лондона. Энергия корреляции для молекулы Н₂, т. е. разность между значениями энергии, получаемыми при расчете по методу МО с самосогласованием и при точном решении уравнения Шредингера (см. стр. 177), составляет около 1,1 эв.

В методе ВС одноэлектронными функциями являются атомные орбитали, а в методе МО - молекулярные орбитали, которые в случае гомоядерных двухатомных молекул распределены поровну между обоими ядрами. Волновые функции молекулы можно построить также из одноэлектронных функций, занимающих промежуточное положение между АО и МО. Например, пусть имеются две одинаковые атомные орбитали, центрированные на разных атомах, φ_а и φ_b. Тогда функции

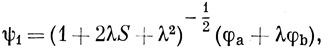
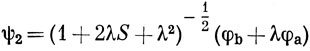
можно назвать эквивалентными делокализованными орбиталями. Если из них достроить функцию Гайтлера - Лондона

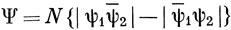
то при λ = 0 получим функцию ВС в простейшей форме, а при λ = 1 - простую МО (см. [15]). Минимизируя энергию по параметру λ, можно найти функцию метода ВС с учетом резонанса ионной и ковалентной структур [см. функцию (12.4)] или МО, в которой учтено конфигурационное взаимодействие [см. функцию (12.5)].

Можно выбрать в уравнении (12.7) параметр К так, чтобы орбитали ψ₁ и ψ₂ были ортогональными. Это свойство орбиталей приводит к значительному упрощению вычислений в многоэлектронной задаче. Условие ортогональности выражается уравнением для λ:

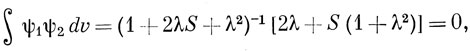
решением которого будет

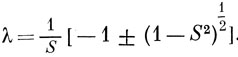
Ортогонализация АО показана на рис. 12.1.

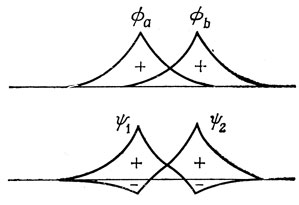
Рис. 12.1. Ортогонализация двух атомных 1s-орбиталей; аргументы волновых функций отсчитываются вдоль межъядерной оси

Ортогонализованные АО можно использовать в качестве базисных функций при построении МО (в виде линейной комбинации ортогонализованных орбиталей), и в случае многоатомных молекул это приводит к полезным упрощениям. При этом важно помнить, что ортогонализация совершенно изменяет характер волновой функции Гайтлера - Лондона. Если с ортогональными орбиталями вычислить обменный интеграл (11.11), то единственным отличным от нуля членом будет двухэлектронный интеграл и потому обменный интеграл А становится положительным. Отсюда следует, что функция Гайтлера - Лондона будет описывать отталкивательное состояние, и если строить функции метода ВС с ортогональными орбиталями, то в волновой функции основного состояния будут преобладать "ионные" функции

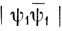
и

Для молекулы водорода из двух 1s-AO можно построить только две независимые волновые функции, описывающие состояние с симметрией ¹∑_g⁺: в методе ВС это функции (12.3) и в методе МО - функции основного и дважды возбужденного состояний. Таким образом, оба метода приводят, как мы видели, к одним и тем же результатам, если в полную волновую функцию включить обе независимые функции. С другой стороны, рассмотрим основное состояние молекулы Не₂. По методу МО оно описывается функцией

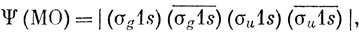
а по методу ВС - функцией

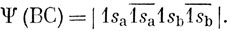
Но эти функции - единственные, какие можно получить рассмотренными двумя методами с использованием только 1s-AO, и потому они должны быть эквивалентными. В этом можно легко убедиться, складывая и вычитая столбцы определителя (12.11) так, чтобы получился определитель (12.12). Таким образом, в случае заполненных оболочек образующих молекулу атомов простейшие волновые функции обоих методов эквивалентны.

В настоящее время в большинстве работ по теории химической связи используется метод МО. Это объясняется тем, что в применении к многоатомным молекулам как самый метод МО, так и программирование расчетов на электронных вычислительных машинах, основанное на этом методе, математически значительно проще и легче, чем метод ВС. Относительная простота метода МО обусловлена тем, что МО, полученные в приближении ЛКАО, взаимно ортогональны. Поэтому матричные элементы гамильтониана, вычисленные с волновыми функциями, построенными из этих орбиталей, можно свести к сумме одно- и двухэлектронных интегралов.

Чтобы проиллюстрировать это, рассмотрим следующий интеграл с функциями, зависящими от координат трех электронов:

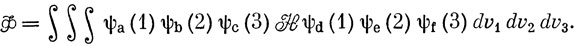
Гамильтониан содержит одно- и двухэлектронные операторы и слагаемое V_nn, выражающее энергию отталкивания ядер [выражение (10.58)]:

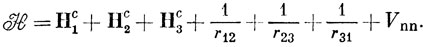
Рассмотрим вклад в выражение (12.13), вносимый оператором H₁^c:

После интегрирования по координатам второго и третьего электронов получим

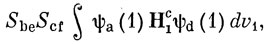
где S - интеграл перекрывания, определенный обычным образом. Если волновые функции построены из ортонормированных МО, то S_bе либо равно нулю

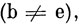
либо - единице

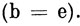
Ясно, что матричные элементы одно-электронных операторов, подобных оператору H₁^c, вычисленные с двумя многоэлектронными функциями, построенными из ортонормированных МО, обращаются в нуль, если эти многоэлектронные функции отличаются более чем одной МО. Подобно этому вклад, вносимый двухэлектронным оператором типа

равен нулю, если обе многоэлектронные функции отличаются более чем двумя орбиталями, и член, выражающий отталкивание ядер, отличен от нуля только в том случае, если многоэлектронные функции одинаковы. Если же набор одноэлектронных функций не является ортонормированным, как это имеет место, например, в методе ВС, то все перечисленные выше упрощения не возникают.

Поэтому расчеты по методу ВС довольно сложны, но результаты, получаемые простым методом ВС, могут оказаться лучше, чем найденные простым методом МО, особенно для энергии диссоциации. В действительности, как будет указано в конце этой главы, наилучшим методом расчета энергии диссоциации в настоящее время является метод атомов в молекулах, представляющий собой модификацию метода ВС.