13.5. Метод МО

Недостатком теории кристаллического поля является ограничение, заключающееся в пренебрежении перекрыванием между орбиталями лигандов и орбиталями переходного металла. Если лиганды неполярны (например, СН₂ = СН₂), то такое перекрывание, вероятно, более существенно, чем электростатическое возмущение. В самом деле, если принять истинные значения потенциала кристаллического поля для полярных лигандов и игнорировать эффекты, связанные с перекрыванием, то количественно трудно получить правильные результаты. Обратимся теперь к методу МО, который учитывает делокализацию электронов переходного металла и лигандов. В сочетании с теорией кристаллического поля такой подход и составляет теорию поля лигандов.

Можно сразу построить МО, беря линейные комбинации орбиталей лигандов и металла. Это потребовало бы решения вековых уравнений с определителями примерно тридцатого порядка. Задача существенно упрощается при использовании теории групп. Сначала построим такие комбинации орбиталей металла, которые преобразуются по НП группы; затем, проделав то же самое для орбиталей лигандов, будем составлять линейные комбинации тех и других функций, которые преобразуются по одинаковым НП.

Мы уже видели, как преобразуются d-орбитали при операциях группы октаэдра. Та же самая процедура может быть использована для других орбиталей этой группы и других возможных групп симметрии комплексов. Результаты, которые могут в дальнейшем понадобиться, приведены в табл. 13.9.

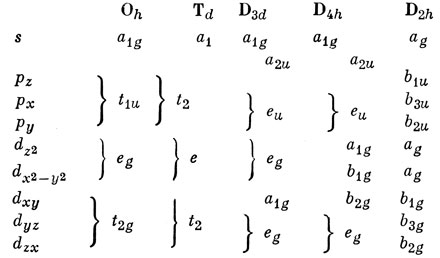
Таблица 13.9. Свойства преобразования атомных орбиталей

Обратимся теперь к орбиталям лигандов, обладающим осевой симметрией (s- и p-орбитали, ориентированные вдоль линии связи с катионом). Сначала нужно выяснить, по какому представлению преобразуются эти орбитали. Пользуясь изложенным ранее методом (т. е. выясняя, сколько орбиталей не изменяются при каждой операции симметрии), находим характеры представления:

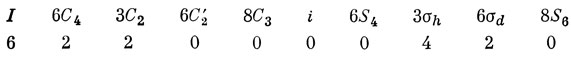
Это приводимое представление разлагается на неприводимые A_1g + Е_g + T_1u.

Чтобы получить линейные комбинации орбиталей лигандов, преобразующиеся по НП группы симметрии O_h (такие комбинации назовем групповыми орбиталями лигандов), воспользуемся методом, изложенным в гл. 8. Берем в качестве исходной одну из орбиталей лигандов и выясняем, как она преобразуется при всех сорока восьми операциях группы симметрии. Обозначим лиганды А → F, как показано на рис. 13.10, и, начиная с лиганда А, получим первую строку табл. 13.10. Чтобы получить, например, групповую t_1u-орбиталь лигандов, умножаем результат применения каждой из операций на соответствующий характер НП Т_1u и полученные результаты складываем. Все эти вычисления приведены в табл. 13.10. Две другие групповые t_1u-орбитали лигандов получаются из рассмотрения преобразований лигандов В или Е и С или F [D снова приводит к ψ' (t_1u)]:

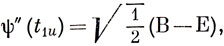
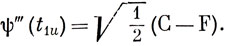
Таблица 13.10. Построение групповых t_1u-орбиталей лигандов

Эти орбитали показаны на рис. 13.11, вместе с соответствующими АО. Очевидно, что обе тройки орбиталей обладают одинаковой симметрией, что отмечено общим символом t_1u.

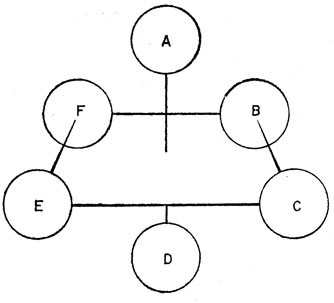
Рис. 13.10. Схема обозначений орбиталей лигандов в октаэдрическом комплексе

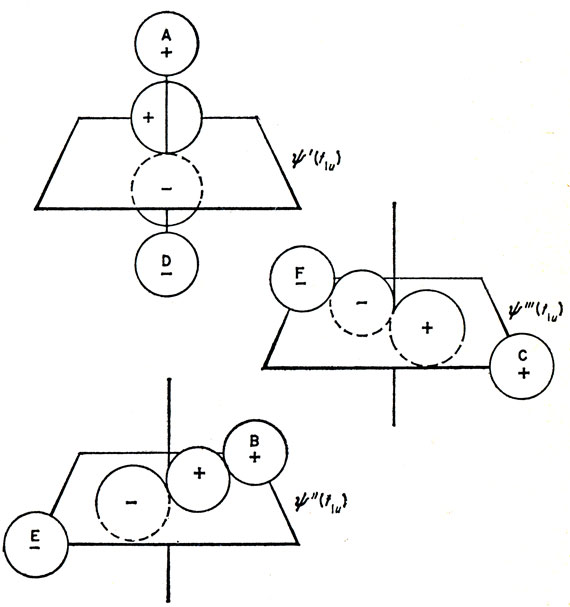
Рис. 13.11. t_1u-Орбитали лигандов

Таким же способом получаются групповые a_1g- и e_g-орбитали:

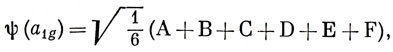
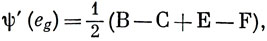
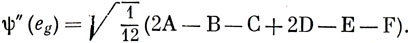
Можно построить три комбинации орбиталей с симметрией e_g, которые подобно d_x², d_y² и d_z² не являются линейно независимыми, но, взяв подходящие линейные комбинации двух из них (см. стр. 145), можно получить две независимые.

Групповые a_1g- и e_g-орбитали показаны на рис. 13.12 вместе со своими аналогами из атомных орбиталей.

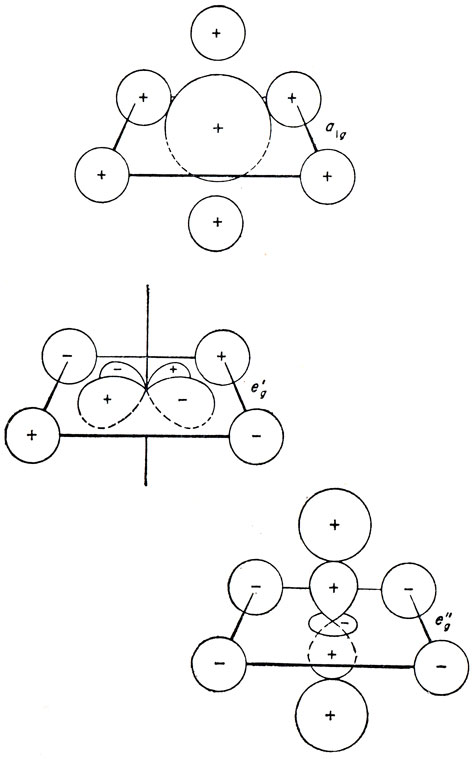
Рис. 13.12. a_1g- и e_g-Орбитали лигандов

Построим теперь диаграмму энергетических уровней МО для комплексов переходных элементов первого ряда (рис. 13.13). Она носит чисто качественный характер. Было предположено, что наиболее существенно взаимодействие между высшими занятыми орбиталями лигандов и частично заполненными d- и незаполненными s- и р-орбиталями катиона. Далее, что орбиталям лигандов соответствует более низкая энергия, чем d-орбиталям катиона. Это предположение подтверждается экспериментальными данными, согласно которым МО, содержащие неспаренные электроны, локализованы главным образом вблизи металла. Порядок расположения разрыхляющих f_1u- и а_1g-орбиталей не известен, но, как будет видно в дальнейшем, он не играет никакой роли в определении свойств симметрии основного состояния. На МО следует поместить двенадцать электронов лигандов и 3d-электроны свободного иона. Низшие a_1g-, t_1u- и e_g-орбитали будут заняты полностью во всех случаях, так что достаточно рассмотреть, как оставшиеся электроны распределены между следующими орбиталями, которыми будут t_2g и е_g^* для состояния с низшей энергией. Именно этот результат был получен в теории кристаллического поля (рис. 13.2), где, однако, не был установлен разрыхляющий характер верхнего уровня. Как при электростатическом подходе, так и при рассмотрении по методу МО, важную роль играет расстояние между расщепленными уровнями t_2g и е_g^*, обозначенное ранее через Δ. Все, что было сказано в теории кристаллического поля относительно состояний комплексов слабых и сильных полей, сохранится и в методе МО.

Рис. 13.13. Диаграмма молекулярно-орбитальной энергии октаэдрического комплекса. Звездочкой отмечены разрыхляющие орбитали

Как было отмечено, t_2g-орбитали являются несвязывающими, однако это перестает быть верным, если существенна π-связь. На рис. 13.14 показаны р-орбитали лигандов, по две для каждого лиганда, которые могут участвовать в образовании π-связи.

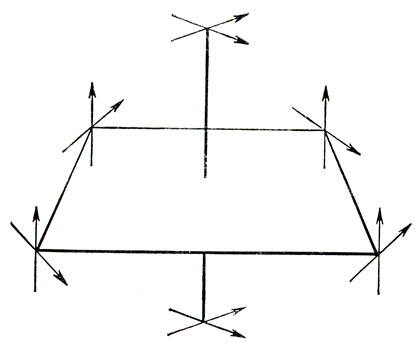
Рис. 13.14. рπ-Орбитали лигандов. Стрелками показаны направления орбиталей, причем конец стрелки соответствует положительному концу орбитали

Из этих π-орбиталей могут быть составлены групповые орбитали лигандов которые в случае симметрии Од преобразуются как T_1g + Т_1u + T_2g + Т_2u. Явный вид этих орбиталей можно определить так же, как это было сделано для σ-орбиталей. Заметим, что на рис. 13.13 нет орбиталей симметрии T_1g и Т_2u, которые являются несвязывающими. Поскольку фактически представляют интерес t_2g- и e_g^*-орбитали, можно не рассматривать групповые π-орбитали лигандов с симметрией t_1u. Остается выяснить, как групповые орбитали лигандов с симметрией t_2g взаимодействуют с несвязывающими t_2g-орбиталями (см. рис. 13.13). По-видимому, возможны два случая: а) лиганд имеет заполненные π-орбитали, которым соответствует более низкая энергия, чем 3d-орбиталям; b) лиганд обладает свободными π-орбиталями с более высокой, чем у 3d-орбиталей, энергией. Энергетические диаграммы для этих двух случаев приведены на рис. 13.15: для (а) в качестве примера взят ион фтора, а для (b) - цианид-ион. Особое внимание следует обратить на различие влияния Δ (см. рис. 13.15). Увеличение Δ при учете π-связи для случая (b), вероятно, объясняет, почему цианид-ион стоит первым в спектрохимическом ряду.

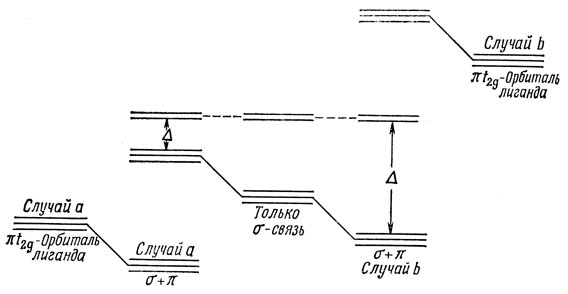
Рис. 13.15. Влияние орбиталей лигандов на молекулярно-орбитальные уровни энергии. Случай а - лиганд имеет заполненные π-орбитали; случай b - лиганд имеет вакантные π-орбитали