13.6. Тетраэдрические и плоские комплексы

Наиболее важными среди комплексов с высокой симметрией, помимо октаэдрических, являются тетраэдрические и плоские квадратные комплексы, которые и обсуждаются ниже. И октаэдр, и тетраэдр можно связать c кубом, как показано на рис. 13.16.

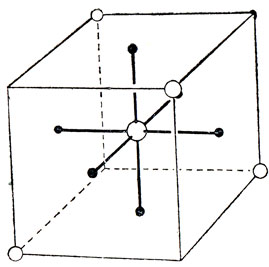
Рис. 13.16. Связь между кубом, октаэдром и тетраэдром

Так же как и в случае октаэдрических комплексов, следует ожидать, что в тетраэдрическом поле d-орбитали разбиваются на две группы: (d_x²-y², d_z²) и (d_xy, d_yz, d_zx) и происходит соответствующее расщепление уровней энергии. В табл. 13.11 приведены характеры НП группы симметрии правильного тетраэдра. Поучительно сравнить эту таблицу с таблицей характеров группы O_h (табл. 13.4).

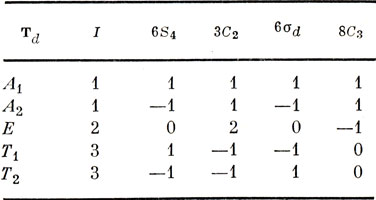
Таблица 13.11. Таблица характеров НП группы симметрии T_d

Приводимое представление, по которому преобразуются d-орбитали, разлагается на Е + T₂. Три р-орбитали образуют базис НП Т₂ (заметьте, не T₁), а s-орбиталь преобразуется по А₁. Поскольку группа T_d не содержит операции инверсии, р- и d-орбитали могут смешиваться. Однако этот эффект крайне мал и здесь он не учитывается. На рис. 13.17 показаны d-орбитали, преобразующиеся по НП Е и T₂. "Лепестки" d_x²-y²-орбитали направлены по линии, проходящей через середину диагонали грани (эта диагональ соединяет два лиганда), а d_xy-орбитали - по линии, проходящей через середину ребра, на котором находится один лиганд. Вероятно, электростатическое отталкивание электрон-лиганд минимально, если электрон занимает d_x²-y²-орбиталь с симметрией е, причем расщепление должно быть меньше, чем в случае октаэдрического поля. Это подтверждается расчетом: в тетраэдрическом поле расщепление составляет 4/9 той величины, которая получается для октаэдрического поля. Очень важно отметить, что t_2g-орбитали имеют более низкую, чем e_g-орбитали, энергию для октаэдра, а t₂-орбиталям в случае тетраэдра соответствует более высокая энергия, чем е_g-орбиталям. Таким образом,

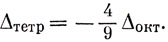
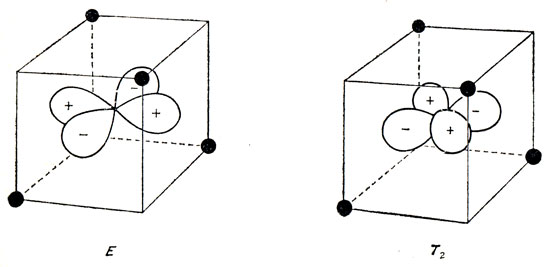
Рис. 13.17. Орбитали симметрии Е и Т₂ в тетраэдрическом поле

На рис. 13.18 представлено соотношение между октаэдрическим и тетраэдрическим расщеплениями для конфигурации (d)¹. Похожая картина наблюдается и для конфигурации (d)⁶; для конфигураций (d)⁴ и (d)⁹ картина обращается. Диаграммы, подобные приведенным на рис. 13.18, часто называют диаграммами Оргела.

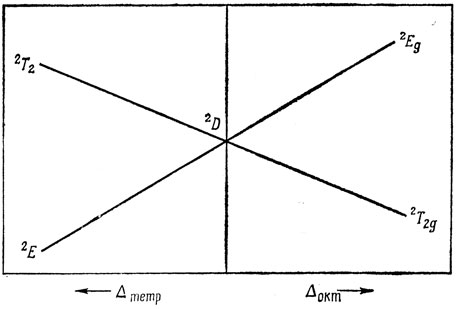
Рис. 13.18. Диаграмма Оргела для конфигурации d¹

Поскольку Δ_тетр составляет около половины Δ_окт для данных иона и лигандов, все тетраэдрические комплексы относятся к высокоспиновым (комплексам слабых полей). Теория кристаллического поля для тетраэдрических комплексов целиком применима к октаэдрическим, только перемена знака Δ вызывает обращение расщеплений. Например, компоненты ³F-терма в конфигурации (d)² для октаэдрического комплекса имеют симметрию: ³Т_1g (основное состояние), ³T_2g (первое возбужденное), ³A_1g (второе возбужденное); в случае же тетраэдрического комплекса основному состоянию соответствует симметрия ³А₁, первому возбужденному - ³Т₂ и второму возбужденному - ³Т₁. Отсюда следует, что в конфигурации (d)² взаимодействие во втором порядке для тетраэдрических комплексов больше, чем для октаэдрических, так как уровни ³Т₁(³F) и ³Т₁(³Р) расположены ближе друг к другу в случае тетраэдрических комплексов. Расчет эффектов второго порядка следует проводить по уравнению (13.17); только члены, содержащие Δ, изменяются таким образом, чтобы уровни энергии в случае предельно сильного поля получались равными

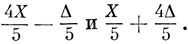
На рис. 13.19 показана диаграмма Оргела для (d)²- и родственных с ней конфигураций.

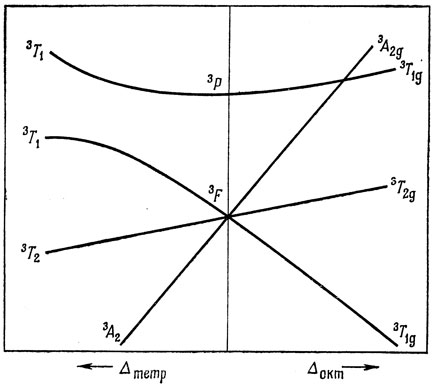
Рис. 13.19. Диаграмма Оргела для конфигурации d²

Как и в случае октаэдрических комплексов, терм ⁶S, соответствующий конфигурации (d)⁵, в тетраэдрическом поле лигандов не расщепляется.

Метод МО становится весьма важным при рассмотрении тетраэдрических комплексов вследствие того, что во многих из них металл имеет высокую валентность (МnО₄^-, МnО₄^2-, СrО₄^2- и т. д.) и следует ожидать значительной делокализации электронов лигандов в сторону катиона. Способ построения групповых орбиталей лигандов, примененный для октаэдрических комплексов, пригоден и для построения тетраэдрических групповых орбиталей лигандов, но включение π-орбиталей чрезвычайно усложняет картину. σ-Орбитали лигандов относятся к типу а₁ и t₂, а π-орбитали - к типу е, t₁ и t₂. Возможные заполненные орбитали ах образуются из а-орбиталей лигандов и s-орбиталей металла, две t₂-орбитали - из σ, π- и р, d-орбиталей лиганда и металла, е-орбиталь - из π- и d-opбиталей лиганда и металла соответственно, а несвязывающая орбиталь t₁ - целиком из π-орбиталей лигандов. В теории кристаллического поля предполагают, что d-орбитали металла с симметрией t₂ вносят основной вклад в низшую разрыхляющую МО t₂ (напоминаем, что по методу МО e_g-орбитали в октаэдрических комплексах являются разрыхляющими орбиталями). Вероятно также и то, что МО с симметрией е является слабо разрыхляющей. На рис. 13.20 приведена обычно принимаемая для тетраэдрических комплексов энергетическая диаграмма, удовлетворяющая перечисленным выше условиям.

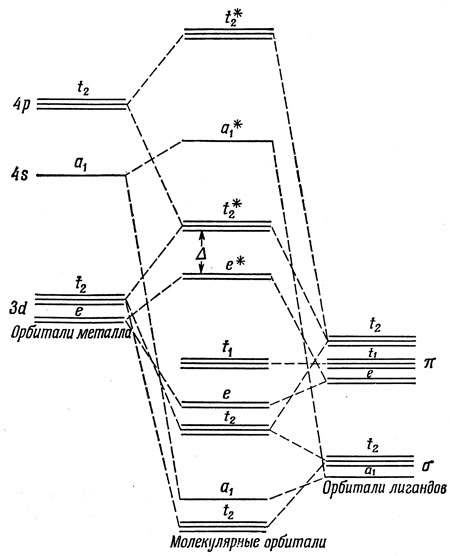
Рис. 13.20. Молекулярно-орбитальная диаграмма для тетраэдрического комплекса, содержащего π-связь

Плоские квадратные комплексы удобнее всего рассматривать как предельный случай тетрагонально искаженных (т. е. растянутых вдоль одной из осей четвертого порядка) октаэдрических комплексов. Если растяжение происходит вдоль оси z, то функция d_xy не относится более к вырожденному состоянию, а состояния d_yz и d_zx по-прежнему являются вырожденными. Снимается также вырождение состояний d_x²-y² и d_z². На рис. 13.21 показано дополнительное расщепление, появляющееся при тетрагональном растяжении октаэдрического комплекса, и связь его с орбиталями в плоском квадратном комплексе.

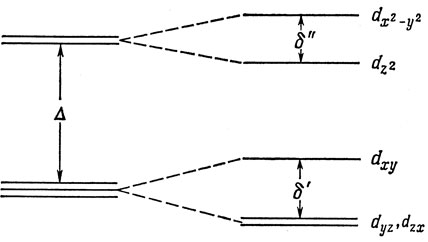
Рис. 13.21. Расщепление d-орбитали при тетраэдрическом искажении октаэдра

Из соображений симметрии не следует равенство δ' и δ". Поэтому приходится вводить два новых параметра, характеризующих расщепление d-уровня, создаваемое тетрагональным полем лигандов. Из рассмотрения интегралов взаимодействия в случае тетрагонального поля можно получить, что δ' = δ".

При интерпретации спектров, обладающих более низкой, чем кубическая, симметрией, оказывается полезным правило "усредненного окружения". Обнаружено, что значение Δ для комплексов МА₃В₃ приблизительно равно среднему арифметическому величин расщепления для МА₆ и МВ₆; для МА₂В₄ - примерно равно 1/3 Δ (МА₆) + 2/3 Δ (МВ₆) и т. д.