
13.7. Эффект Яна - Теллера
Существует общая теорема, полученная Яном и Теллером, которая утверждает следующее: в вырожденном электронном состоянии конфигурация нелинейной молекулярной системы изменяется так, чтобы вырождение оказалось снятым. Проиллюстрируем это на следующем примере. Двухвалентный атом меди имеет конфигурацию (d)9, и в октаэдрическом комплексе получается электронная конфигурация t2g6eg3, которая дает 2Eg-состояние. В этом состоянии дырка на еg-орбитали может быть отнесена как к dz2-, так и к dx2-y2-орбиталям. Теорема Яна - Теллера требует такого искажения октаэдрической симметрии, которое устраняет вырождение. Если это происходит в результате тетрагонального растяжения вдоль оси z, то дырка будет локализована на орбитали dx2-y2. Если же наблюдается тетрагональное сжатие вдоль оси z, то дырка локализуется на орбитали dz2. Теорема Яна - Теллера не позволяет установить, какое из этих двух искажений происходит (или же имеет место какое-либо другое искажение). Детальные расчеты показывают, что тетрагональное растяжение более вероятно, и этот вывод подтверждается данными рентгенографического исследования. Аксиальные связи в октаэдрических комплексах меди почти всегда длиннее экваториальных.
Пользуясь теорией групп, можно выяснить, как уровни состояний, отвечающих октаэдрическому комплексу, расщепляются при понижении симметрии. Для нескольких наиболее важных случаев это показано в табл. 13.12. Отсюда еще не ясно, почему такое расщепление приводит к более стабильному основному состоянию.
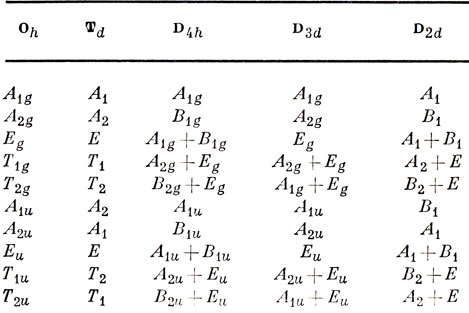
Таблица 13.12. Корреляция между НП октаэдрической, тетраэдрической и других групп с более низкой симметрией
Допустим, что мы исходим из правильного октаэдрического комплекса в равновесной конфигурации. Любое искажение этой конфигурации можно выразить через координаты симметрии R, которые преобразуются по НП группы и являются линейными комбинациями координат, выражающих валентное и деформационное смещения. Например, для координат симметрии A1g имеем
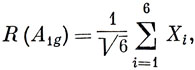
где Xi - изменение длины i-й связи. Если H - гамильтониан неискаженной молекулы, то, применяя разложение в ряд Тейлора, для гамильтониана искаженной молекулы получаем
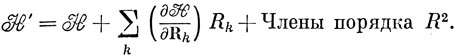
Затем волновые функции искаженной молекулы представляют в виде линейной комбинации функций, соответствующих неискаженной молекуле, и решают вековое уравнение |H'rs - ESrs| = 0. Оказывается, что существует по крайней мере одна координата симметрии Rk, которая входит линейно в энергию основного состояния (или же две координаты Rk1 и Rk2, входящие в выражение для энергии в виде [Rk12 + Rk22]1/2, где Rk1 и Rk2 преобразуются по одному и тому же многомерному НП группы симметрии). Это означает, что, помимо квадратичных членов, в потенциальную энергию входит линейный по смещению член и, следовательно, минимум энергии не соответствует октаэдрической симметрии.
В химии комплексов переходных металлов эффект Яна - Теллера является существенным лишь в случае неодинаковой занятости еg-орбиталей. Хотя неодинаковое заполнение t2g-орбиталей также должно привести к искажению, несвязывающий характер этих орбиталей способствует тому, что такое искажение комплекса будет малым. Практически обычно существуют другие причины, устраняющие вырождение этих орбиталей (например, спин-орбитальное взаимодействие или кристаллические силы).
Если изменение энергии вследствие эффекта Яна - Теллера одного порядка величины с нулевой колебательной энергией, то постоянное искажение молекулы не имеет места. Это связано с тем, что приближение Борна - Оппенгеймера перестает быть справедливым, и в этом случае говорят о динамическом эффекте Яна - Теллера.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'