
13.8. Электронные спектры комплексов переходных металлов
В видимой и ультрафиолетовой областях спектра для комплексов переходных металлов наблюдают полосы трех типов:
а) узкая, слабая;
б) широкая, слабая;
в) широкая, интенсивная.
Полосы первых двух типов объяснены в теории кристаллического поля; для интерпретации полос третьего типа требуется теория поля лигандов.
Все слабые полосы возникают в результате запрещенных электронных переходов, при которых электрон возбуждается с одной d-орбитали на другую. Эти переходы известны как g → g-переходы (см. стр. 170). Относительное расположение слабых полос довольно хорошо коррелирует с диаграммами энергетических уровней, которые показаны на рис. 13.6-13.9.
Интенсивные широкие полосы, которые обычно наблюдают в коротковолновом конце спектра, обусловлены переходами электрона с одной из связывающих МО (локализованной в основном на лигандах) на другую eg- или t2g-орбиталь, локализованную главным образом на металле. Такие переходы сопровождаются переносом заряда от лигандов к металлу и называются переходами с переносом заряда (см. гл. 18). Широкие интенсивные полосы мало изучены, хотя для некоторых комплексов обнаружена корреляция между положением полос и природой лиганда. Легче всего провести количественную интерпретацию спектров комплексов слабых полей. В промежуточных случаях, часто встречающихся на практике, существенны эффекты второго порядка и необходимо решать вековые уравнения высоких степеней (например, вековое уравнение из определителя десятого порядка в уже упоминавшемся случае 2Т2(5)-состояния) *).
*) (Матрицы взаимодействия приведены в работах [57, 81], и в них надо подставить только числа, соответствующие рассматриваемому иону. Решение вековых уравнений высоких порядков - задача, требующая применения вычислительных машин.)
Обсудим спектры двух ионных комплексов [Ti(H2O)6]3+ и [V(H2O)6]3+ (с конфигурациями (d)1 и (d)2 соответственно). Спектр комплекса [Ti(H2O)6]3+ показан на рис. 13.22. В нем имеется один слабый пик при 20300 см-1, приписываемый переходу 2T2g → 2Eg; это число и дает величину А, выраженную в см-1. В большинстве октаэдрических комплексов иона Ti3+ этот слабый пик имеет ступеньку, иногда почти разрешаемую как отдельный пик. Появление ее вызвано, по-видимому, тем, что для возбужденного уровня имеет место эффект Яна - Теллера вследствие того, что на еg*-орбиталях находится один электрон. Спектр поглощения комплекса [V(H2O)6]3+ показан на рис. 13.23. В нем наблюдают два слабых пика при 17100 и 25200 см-1, приписываемые переходам 3T1g → 3T2g и 3T1g → 3T1g.
![Рис. 13.22. Спектр поглощения комплекса [Ti(H2O)6]3+ и интерпретация этого спектра](pic/000642.jpg)
Рис. 13.22. Спектр поглощения комплекса [Ti(H2O)6]3+ и интерпретация этого спектра
![Рис. 13.23. Спектр поглощения комплекса [V(H2O)6]3+ и интерпретация этого спектра](pic/000645.jpg)
Рис. 13.23. Спектр поглощения комплекса [V(H2O)6]3+ и интерпретация этого спектра
Используя полученные ранее формулы (стр. 298 и табл. 13.6), можно вывести два уравнения
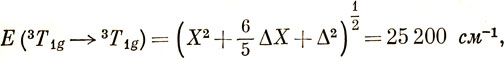
E (3T1g → 3T2g) = - 1/2 X + 1/2 Δ + 1/2 (Х2 + 6/5 Δ Х + Δ2)1/2 = 17100 см-1,
решение которых дает Δ = 16700 см-1, X = 11800 см-1. Найденное значение X сравним с расстоянием между уровнями 3F и 3Р в свободном ионе, равным 13200 см-1. Согласие между этими двумя значениями определяет применимость приближения кристаллического поля. Для перехода 3T1g → 3Ag вычисленное положение пика составляет 34100 см-1. Эта область перекрывается интенсивной полосой, обусловленной переходом с переносом заряда.
Из рис. 13.8 видно, что при конфигурации (2)3 энергия трех из возбужденных состояний характеризуется примерно той же зависимостью от величины Δ, что и энергия основного состояния; для остальных возбужденных состояний эта зависимость совершенно иная. Поскольку величина Δ модулируется тепловыми колебаниями лигандов (сжатому комплексу соответствуют большие значения Δ, а растянутому - меньшие), можно считать, что для переходов, подобных 4A2g → 2E2g, энергия которых почти не зависит от Δ, будут наблюдаться более узкие полосы, чем для переходов, например 4A2g → 4T2g, энергия которых очень чувствительна к величине Δ. Это явление хорошо заметно на спектре поглощения кристалла рубина (Сr2O3, Аl2O3), представленном на рис. 13.24. Все узкие полосы запрещены по спину, так как в основном и возбужденном состояниях одинаково заполнение eg- и t2g-орбиталей вследствие того, что энергии их равным образом зависят от Δ, а отличие их - только в спиновой мультиплетности. Однако обратная картина неверна - не все запрещенные по спину переходы дают узкие полосы.
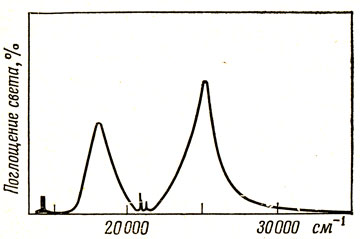
Рис. 13.24. Спектр поглощения рубина
Полагают, что интенсивность слабых полос поглощения определяется в основном d - р-смешиванием. Если имеет место d - р-смешивание, то переходы d → d в некоторой степени приобретают характер переходов d - р и р → d, которые разрешены как в свободном ионе, так и в комплексе. В тетраэдрических комплексах, например, р- и три d-орбитали преобразуются по представлению T2, так что смешивание возможно. Поэтому в тетраэдрических комплексах наблюдают значительно более интенсивные полосы поглощения, чем в октаэдрических; хороший пример тетраэдрического комплекса с сильным поглощением представляет ион марганца в поде лигандов. Второй полезный пример - сравнение спектров комплексов [СоСl4]2- (ярко-голубой) и [Со(Н2O)6]2- (бледно-розовый). Это все же не объясняет спектры строго октаэдрических комплексов, в которых d - р-смешивание невозможно. Правда, предлагаемая нами модель не является полной, потому что в ней не учитываются колебания молекулы. Некоторые из этих колебаний приводят к снижению симметрии, которое делает допустимым d - p-смешивание. Интенсивность полосы поглощения в действительности следует определять путем усреднения по всем конфигурациям, которые принимает молекула в процессе колебаний.
Переходы между состояниями с различной спиновой мультиплетностью запрещены в отсутствие спин-орбитального взаимодействия (стр. 169). При наличии спин-орбитального взаимодействия S перестает быть "хорошим" квантовым числом и переходы между состояниями с различной спиновой мультиплетностью способствуют возникновению слабых полос поглощения.
Существуют также другие физические явления, которые могут пролить свет на природу комплексов металлов. Во-первых, магнитные измерения объемной восприимчивости и электронного спинового резонанса позволяют непосредственно определить симметрию основного состояния. Во-вторых, изучение поглощения поляризованного света кристаллом и - для оптически активных комплексов - исследование кругового дихроизма и дисперсии оптического вращения дают дополнительную информацию о возбужденных состояниях. Хотя эти методы и очень важны, по нашему мнению, их рассмотрение выходит за рамки этой книги.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'