
15.2. Метод МО в приближении Хюккеля
Хюккель предложил очень простую форму метода МО, которая оказалась весьма ценной при установлении корреляции свойств ненасыщенных органических молекул. Уравнения вида (15.2) упрощаются при введении следующих приближений:
1. Интегралы перекрывания считаются равными нулю даже для АО, относящихся к соседним атомам, т. е. Sμν = 0 при μ ≠ ν. Всегда можно взять нормированные АО, т. е. считать Sμμ = 1.
2. Интегралы Нμμ полагаются одинаковыми для всех атомов. Их обозначают буквой а и называют кулоновскими интегралами.
3. Интегралы Нμν принимаются одинаковыми для всех пар связанных непосредственно между собой атомов с номерами μ и ν (т. е. соседние атомы, изображаемые μ → ν). Их обозначают буквой β и называют резонансными интегралами.
4. Интегралы Нμν = 0 для непосредственно не связанных между собой атомов.
При этих предположениях уравнения (15.2) можно переписать в виде
cμ (α - E) + ∑ν→μ сν β = 0 (15.3)
или, вводя величину
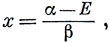
в виде
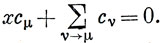
Простейшая из молекул, к которой применимо предыдущее рассмотрение, - молекула этилена. Обозначим атомы углерода цифрами 1 и 2 и получим систему уравнений (см. задачу 10.6):
μ = 1, хс1 + с2 = 0.
μ = 2, с1 + xс2 = 0.
Эти два уравнения имеют нетривиальное решение, если определитель из коэффициентов с равен нулю (стр. 109), т. е.
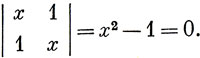
Решения полученного уравнения х = ± 1 дают Е = α + β или Е = α - β соответственно.
Подставляя в систему двух уравнений х = -1, находим
с1 = с2.
Применяя условие нормировки, можно записать
c12 + c22 = 1.
В приближении нулевого перекрывания члены, содержащие c1c2, не появляются, и мы приходим к решению
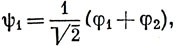
E1 = α + β.
Аналогично, подставляя x = 1 в вековые уравнения, получим второе решение
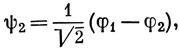
Е2 = α - β.
Резонансный интеграл β - отрицательная величина, приблизительно равная энергии заряда, распределенного с плотностью φμφν в поле ядер, экранированных σ-электронами *). Функция ψ1 характеризуется более низкой энергией электрона, чем в изолированном атоме углерода (величина а в приближении Хюккеля), и поэтому она является связывающей МО; ψ2 - разрыхляющая орбиталь, так как ей соответствует более высокая, чем в изолированном атоме, энергия электрона. На рис. 10.3 схематически изображены формы этих орбиталей.
*) (См. примечание на стр. 190. - Прим. ред.)
Более интересный пример представляет молекула бутадиена
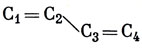
Уравнения для орбитальных коэффициентов имеют вид *)
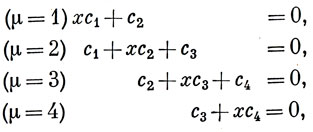
а вековой определитель -
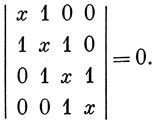
*) (В этом приближении не существует разницы между уравнениями для цис- и транс-бутадиена.)
Раскрывая определитель, получаем уравнение x4 - 3x2 + 1 = 0, которое имеет решения х = ± 1,62, x = ± 0,62.
Возьмем одно из этих решений (х = - 1,62) и, подставляя его в систему (15.6), найдем
(μ = 1) с2 = 1,62 c1,
(μ = 2) с3 = - c1 + 1,62 с2 = 1,62 с1,
(μ = 3) с3 = 1,62 с4, т. е. c4 = c1.
Из условия нормировки
c12 + c22 + c32 + c42 = 1
имеем
c1 = ± 0,37.
Поскольку знак волновой функции выбирается произвольно, можно взять с1= + 0,37, и тогда получим
ψ1 = 0,37ψ1 + 0,60ψ2 + 0,60ψ3 + 0,37ψ4; E1 = α + 1,62 β.
Аналогичным путем можно найти остальные три МО и соответствующие им энергии:
ψ2 = 0,60ψ1 + 0,37ψ2 - 0,37ψ3 - 0,60ψ4; E2 = α + 0,62 β.
ψ3 = 0,60ψ1 - 0,37ψ2 - 0,37ψ3 + 0,60ψ4; E3 = α - 0,62 β.
ψ4 = 0,37ψ1 - 0,60ψ2 + 0,60ψ3 - 0,37ψ4; E4 = α - 1,62 β.
Эти орбитали показаны схематически на рис. 15.1.
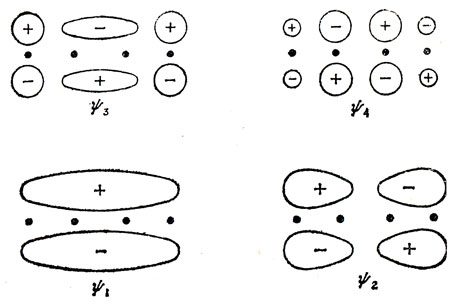
Рис. 15.1. Хюккелевские орбитали бутадиена
Нумерация функций ψ1 ... ψ4 соответствует возрастанию значений энергии, и в основном состоянии π-электроны заполняют связывающие орбитали ψ1 и ψ2. Основному состоянию отвечает конфигурация ψ12ψ22 и волновая функция представляется слэтеровским определителем |ψ1ψ‾1ψ2ψ‾2| (см. разд. 7.1).
Хотя в разд. 10.5 уже говорилось, что при надлежащем учете межэлектронного взаимодействия сумма орбитальных энергий не равна полной электронной энергии, тем не менее можно надеяться, что по крайней мере приближенно эти величины коррелируют. По этой причине полная энергия молекулы, вычисленная в приближении Хюккеля, - полезная величина. Сумма хюккелевских энергий четырех электронов для основного состояния молекулы бутадиена равна 2 (α + 1,62 β) + 2 (α + 0,62 β) = 4α + 4,48β. Энергия двух локализованных π-связей, согласно расчету молекулы этилена, равна 4α + 4β, и поэтому 0,48β представляют собою понижение энергии, обусловленное делокализацией электронов *). Эта величина является аналогом энергии резонанса в методе ВС.
*) (Эти рассуждения справедливы только в том случае, если значения интеграла β одинаковы для молекул этилена и бутадиена. Это означает, что энергия делокализации вычислена по отношению к π-электронной энергии двух молекул этилена, имеющих такие же длины связей, как средняя длина связи в молекуле бутадиена.)
Как будет указано в следующей главе, электронные плотности играют важную роль при интерпретации реакционной способности органических соединений. Электронная плотность, соответствующая орбитали ψr = ∑μ crμ φμ, равна ∑μ crμ2 φμ2 (в пренебрежении всеми плотностями перекрывания типа φμφν). Можно сказать, что crμ2 есть мера заряда, вносимого на атом с номером μ электроном, занимающим орбиталь ψr. Просуммировав по всем занятым орбиталям (на каждой из них по 2 электрона), получим полный π-электронный заряд на атоме μ
qμ = 2 ∑r зан сrμ2. (15.8)
Для бутадиена, например, q1 = 2с112 + 2с212 = 2 (0,37)2 + 2 (0,60)2 = 1,00 и q2 = 2c212 + 2с222 = 2 (0,60)2 + 2 (0,37)2 = 1,00. В силу симметрии атомы 3 и 4 имеют тот же самый заряд, что и атомы 2 и 1, и, следовательно, π-электронный заряд на всех атомах углерода равен единице.
Другой важной величиной является порядок π-электронной связи (иногда его называют порядком подвижной связи), определяемый следующим образом:
pμν = 2 ∑r зан сrμ crν. (15. 9)
Если атом μ, непосредственно связан с атомом ν, то порядок связи характеризует плотность π-электронного заряда на связи. Для бутадиена, например,
p12 = 2с11c21 + 2с12с22 = 2 (0,37 · 0,60) + 2 (0,60 · 0,37) = 0,89
и
p23 = 2с21c31 + 2с22с32 = 0,45; p34 = p12 (в силу симметрии).
В этилене порядок π-электронной связи равен 1; поэтому чем ближе к единице порядок связи, тем связь ближе к двойной. Как видно, в приближении Хюккеля центральная связь в бутадиене имеет значительно меньшую степень двоесвязности, чем крайние связи, что находится в соответствии с обычным представлением молекулы бутадиена одной валентной схемой с единичной средней связью.
Экспериментально найдено, что порядок π-электронной связи и длина связи коррелируют друг с другом, как это показано на рис. 15.2. Единственными соединениями, в которых порядок связи определяется симметрией, а не зависит от приближения Хюккеля, являются графит (0,525), бензол (0,667) и этилен (1,0). Беря длины связей в этих трех соединениях равными 1,421, 1,397 и 1,344 А соответственно, можно получить, что между длиной связи R и порядком связи р существует линейная зависимость, определяемая выражением
R(А) = 1,50 - 0,16 р. (15.10)
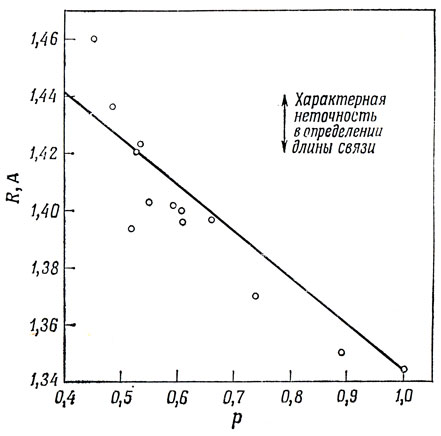
Рис. 15.2. Корреляция между порядком и длиной связи
Из рис. 15.2 видно, что и для других соединений это соотношение выполняется довольно хорошо. Для описания зависимости между R и р было предложено несколько нелинейных соотношений, но если учитывать, что неточность экспериментальных измерений длин связей обычно величина порядка 0,02 А, то очевидно, что экспериментальные данные недостаточно точны, чтобы подтвердить такие нелинейные соотношения.
Орбитальная энергия в приближении Хюккеля равна
Еr = ∫ ψr H ψr dυ = ∫ (∑μ сrμ φμ) Н (∑ν crν φν) dυ = ∑μ crμ2 α + 2 ∑ν→μ crμ crν β. (15.11)
Полная энергия по Хюккелю получается суммированием по всем заполненным орбиталям:
ε = 2 ∑r Er = 2 ∑r (∑μ crμ2 α + 2 ∑ν→μ crμ crν β) = ∑μ qμ α + 2 ∑ν→μ pμν β. (15.12)
Таким образом, полная энергия выражается через π-электронные заряды и порядки связей. В случае конфигураций с незаполненными оболочками q и р обобщаются следующим образом
qμ = ∑r nr cμr2,
pμν = ∑r nr cμr cνr,
где nr - число электронов на орбитали ψr.
Имеется еще одна величина, оказавшаяся полезной в теории молекул, - это индекс свободной валентности, введенный Коулсоном, определяемый по формуле
Fμ = nmax - nμ, (15.13)
где nμ - сумма порядков всех подвижных связей, исходящих из атома μ, a nmax - максимальное значение такой суммы [обычно его принимают равным √3 - значению для центрального атома в гипотетической молекуле (СН2)3С; см. задачу 15.1]. Для бутадиена F1 = F4 = 1,73 - 0,89 = 0,84 и F2 = F3 = 1,73 - 0,89 - 0,45 = 0,39. Эту величину в методе МО можно рассматривать как эквивалент остаточного сродства по Тиле. Обычное значение F для атома углерода в ароматических молекулах равно примерно 0,4, а в свободном радикале, в котором неспаренный электрон принадлежит практически одному атому, F ≈ 1. Как будет видно из гл. 17, индекс свободной валентности коррелирует с реакционной способностью атома в молекуле при атаке свободным радикалом.
Все наше описание π-электронов в молекуле бутадиена можно суммировать в виде следующей диаграммы:
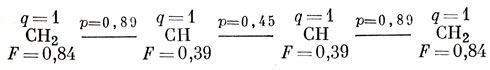
Отметим два важных свойства орбиталей в молекуле бутадиена. Во-первых, они разбиваются на пары (с энергиями α ± xβ), и, во-вторых, коэффициенты спаренных (орбиталей или совпадают, или отличаются знаком. Эти свойства характерны вообще для всех так называемых альтернантных углеводородов. К альтернантным углеводородам относят молекулы с сопряженными связями, в которых атомы углерода можно разбить на два набора (помеченные звездочкой и не помеченные) таким способом, что никакие два атома из одного и того же набора не являются соседними (фактически, это означает, что циклическими неальтернантными соединениями являются только углеводороды с нечетным числом атомов в кольце, например, такие, как азулен).
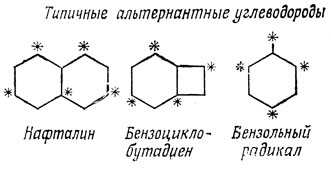
В альтернантных углеводородах с нечетным числом атомов, участвующих в сопряжении (например, бензильный радикал) помечают атомы большего набора.
Общий вид уравнений для орбитальных коэффициентов в приближении Хюккеля был записан в виде (15.5):
х сμ + ∑ν→μ cν = 0.
Для альтернантных углеводородов, если μ - номер атома из помеченного набора, ν обязательно нумерует атом из непомеченного набора. Так, если хr, сrμ и crν относятся к одному решению этих уравнений, то
хr сrμ + ∑ν→μ crν = 0. (15.14)
Но, очевидно,
(-хr) сrμ + ∑ν→μ (-crν) = 0,
и, следовательно, орбиталь с -хr, сrμ и -crν также должна быть решением этих уравнений. Таким образом, если ψr - связывающая орбиталь с энергией α - xβ, существует также разрыхляющая орбиталь ψ-r с энергией α + хβ. Более того, если связывающая орбиталь имеет вид
ψr = ∑μ* crμ φμ + ∑ν° crν φν, (15.15)
где суммирование по наборам помеченных и непомеченных атомов обозначено ∑* и ∑° соответственно, спаренная с ней разрыхляющая орбиталь запишется как
ψr = ∑μ* crμ φμ - ∑ν° crν φν. (15.16)
Итак, чтобы построить разрыхляющую орбиталь, можно просто изменить знаки у коэффициентов при АО непомеченных атомов в связывающей орбитали.
Нейтральные альтернантные углеводороды обладают еще одним свойством, которое уже было отмечено на примере бутадиена, - π-электронный заряд, определенный по уравнению (15.8), для всех атомов равен единице. Для доказательства этого заметим, что для любого ортонормированного набора МО
∑μ* crμ2 = 1. (15.17)
Однако в силу свойства парности орбиталей в альтернантных углеводородах
∑r зан crμ2 = ∑r незан crμ2.
Отсюда
2 ∑r зан crμ2 = 1. (15.18)
Поэтому альтернантные углеводороды неполярны в согласии с тем экспериментальным фактом, что для молекул, подобных фенантрену, не обнаружен дипольный момент; в противоположность этому неальтернантные углеводороды, как, например, азулен или фульвен, обладают заметными дипольными моментами.
|
ПОИСК:
|
© CHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://chemlib.ru/ 'Библиотека по химии'