15.3. Использование симметрии при построении орбиталей в приближении Хюккеля

Метод построения хюккелевских МО, изложенный в общих чертах при рассмотрении бутадиена, можно применять к любым молекулам с сопряженными связями. Однако для больших молекул подобные расчеты, хотя они и не представляют принципиальных затруднений, становятся чрезвычайно громоздкими, если не использовать вычислительных машин. Если молекула обладает симметрией, то ее можно использовать для упрощения вычислений. Это упрощение состоит в том, что вековой определитель представляется в виде произведения определителей более низких порядков. Например, для молекулы нафталина при построении хюккелевских орбиталей получаем определители десятого порядка; используя симметрию молекулы, приходится иметь дело с вычислением определителей порядка не выше третьего.

Молекула нафталина относится к группе симметрии D_2h (см. табл. 14.1). Одна половина НП этой группы соответствует симметрии по отношению к отражению в плоскости yz, другая - антисимметрии. МО типа σ относятся к первому классу, а типа π - ко второму. Если ограничиться рассмотрением лишь π-орбиталей, то можно видеть, что они отличаются друг от друга поведением при трех операциях поворота вокруг осей второго порядка. Таким образом, все π-орбитали можно разделить на различные по свойствам симметрии группы, рассматривая только подгруппу операций I, С₂^z, С₂^y, С₂^x, т. е. группу D₂, характеры НП которой приведены в табл. 15.1.

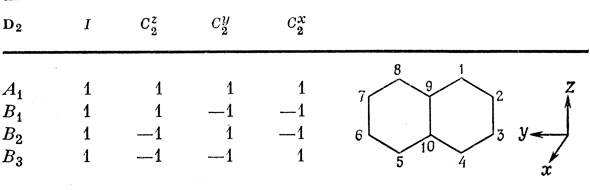
Таблица 15.1. Таблица характеров группы D₂

Чтобы найти типы симметрии π-МО в этой подгруппе, воспользуемся изложенным ранее (стр. 140-143) методом и выясним, сколько из десяти р_х-АО остаются неизменными при операциях группы, Это дает следующее представление Г, базис которого образуют указанные десять орбиталей:

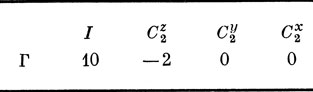
Разложим приводимое представление Г на неприводимые; вычисляя скалярные произведения характеров этого представления на характеры НП группы (трактуя ряды чисел как компоненты четырехмерного вектора)

и деля эти числа на порядок группы (4), получим число молекулярных орбиталей, которые преобразуются по НП: 2А₁ + 2В₁ + 3B₂ + 3B₃. По отношению к полной группе D_2h это разложение имеет вид 2A_u + 2B_1g + 3B_2g + 3B_3u.

Выясним теперь вид хюккелевских орбиталей с такими свойствами симметрии; из рассмотрения таблицы характеров легко получить следующие диаграммы:

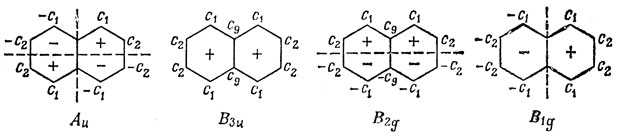
Орбитали, преобразующиеся по НП А_u, обладают узловой плоскостью xy и xz, так как они симметричны относительно поворотов С₂^y и С₂^z (нужно помнить, что мы имеем дело с р_x-АО, которые антисимметричны относительно отражения в плоскости yz). Это означает, что не известны лишь два коэффициента с₁ и с₂ в любой из орбиталей симметрии А_u. Из сказанного выше можно видеть, что каждое НП входит в представление Г, базисом которого являются десять хюккелевских орбиталей, столько раз, сколько различных неизвестных хюккелевских коэффициентов содержат орбитали, преобразующиеся по НП. Это означает, что можно было бы определить число различных МО каждой симметрии, просто рисуя диаграммы для каждого из типов симметрии и определяя для них число неизвестных коэффициентов.

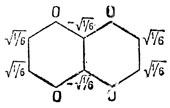
Получим теперь вековые определители для каждого типа симметрии. Общее число уравнений для орбитальных коэффициентов равно десяти, но их можно разбить на три независимые группы, т. е. в молекуле содержатся атомы только трех различных типов. Пусть, например, имеется [уравнение (15.5) и рисунок к табл. 15.1]

и аналогичное уравнение, содержащее хс₁₀. Два других уравнения есть

Если теперь воспользоваться симметрией МО, то можно увидеть, что этих трех уравнений достаточно для определения орбитальных коэффициентов энергий.

Например, в орбиталях симметрии B_3u с₁ = с₈ = с₄ = c₅, с₂ = с₃ = c₆ = с₇, с₉ = с₁₀ и, следовательно, уравнения (15.19) для них имеют вид

а соответствующее вековое уравнение -

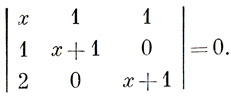
Раскрывая определитель, имеем уравнение

из которого получаем

Беря, например, решение x = -1 и подставляя его в уравнения (15.20), находим

Из соображений симметрии с₄ = с₅ = c₈ = 0, с₃ = c₆ = с₇ = с₂ и с₉ = с₁₀. Учитывая условие нормировки 6с₂² = 1 и помня, что волновая функция в целом определена лишь с точностью до знака, получим интересующую нас МО

Коэффициенты в других орбиталях симметрии В_3u получаются таким же образом.

Таким же способом можно построить МО, относящиеся к другим типам симметрии. Соответствующие вековые определители имеют вид

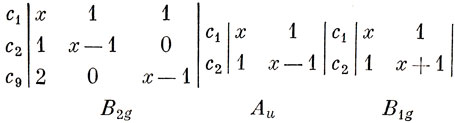
Коэффициенты связывающих МО и соответствующие им хюккелевские энергии приведены в табл. 15.2. Молекула нафталина относится к альтернантным углеводородам, и поэтому для получения соответствующих разрыхляющих орбиталей достаточно изменить знаки коэффициентов для каждого второго атома (связывающая B_3u-орбиталь становится B_2g-разрыхляющей, связывающая B_1g-орбиталь - A_u-разрыхляющей, и наоборот).

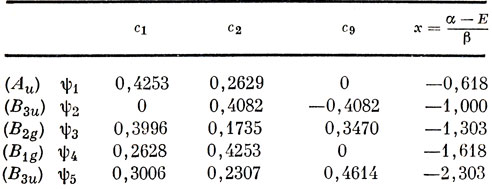
Таблица 15.2. Коэффициенты связывающих орбиталей и хюккелевские энергии