15.4. Циклические сопряженные полиолефины и хюккелевское правило 4n + 2

Уравнения для орбитальных коэффициентов в случае циклического полиолефина имеют вид [см. уравнение (15.5)]

где μ - 1, μ и μ + 1 - номера трех следующих друг за другом атомов кольца. Отыскивая общее решение для коэффициентов с_μ, нужно наложить условие периодичности по t (t - число атомов в кольце). В качестве пробного решения возьмем с_μ = sin kμ, где

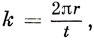
r - целое число. Эта функция удовлетворяет граничному условию c_μ = c_t+μ. Подставляя ее в уравнение (15.21), получим

Используя равенство

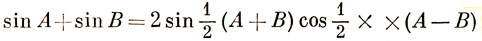
и объединяя первый и последний члены в выражении (15.22), получим

Следовательно, х = -2 cos k:, т. е.

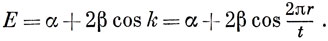
Если число атомов в кольце четное, то возможны решения при

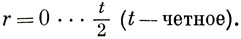
Если число атомов нечетное, то

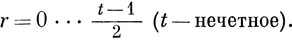
Очевидно, рассматриваемая нами функция удовлетворяет уравнению, так же как и решение с_μ = cos kμ. В этом случае можно написать

Используя равенство

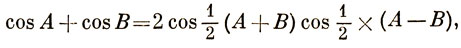
имеем

что приводит к тем же значениям энергии [см. уравнение (15.24)].

Таким образом, для всех значений r, кроме r = 0 или

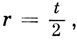
при четном числе атомов в кольце, когда решение в виде синуса обращается в нуль, существует два решения уравнения (15.21). Это означает, что низшая орбиталь в циклическом полиолефине не вырождена, но все орбитали с более высокой энергией двукратно вырождены, за исключением высшей орбитали при четном t. Этот результат можно представить геометрически, как это сделано на рис. 15.3. Для получения энергетических уровней циклической системы из t атомов в приближении Хюккеля, впишем правильный многоугольник с t сторонами в круг радиуса 2β так, чтобы одна из вершин была в самой низкой точке. Каждая из остальных вершин соответствует одной хюккелевской орбитали, энергия которой определяется в единицах β расстоянием от горизонтального диаметра круга (задача 15.8).

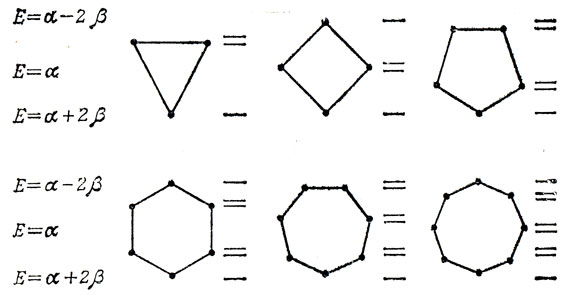
Рис. 15.3. Схема энергетических уровней циклических полиенов

Поскольку на каждой орбитали может быть два электрона, только циклические ненасыщенные молекулы, имеющие (4n + 2) π-электрона, будут иметь электронную конфигурацию с замкнутой оболочкой и поэтому окажутся химически стабильными. Соединения с (4n + 1) π-электронами будут свободными радикалами, а для соединений с 4n π-электронами основное состояние является триплетным.

Связь между этим правилом и ароматичностью приводит к довольно запутанным выводам. Бензол является прототипом ароматического соединения, поэтому ароматичность соединения определяется тем, в какой степени его свойства напоминают свойства бензола.

Существует тенденция называть ароматическими соединения, которые вовсе не обладают химическим сходством с бензолом, а только удовлетворяют правилу 4n + 2. Исключительная стабильность молекулы бензола объясняется тем, что внутренний угол правильного шестиугольника равен 120°, и поэтому в связях sp²-гибридизованных атомов углерода не возникает напряжения.

Для аниона циклопентадиенила С₂Н₅^-, радикала С₅Н₅^. и катиона С₅H₅⁺ в методе ВС требуется принять по крайней мере пять эквивалентных структурных схем, чтобы объяснить эквивалентность атомов углерода. Если использовать простейший подход и отождествить стабильность с числом структурных схем, то можно будет заключить, что все эти соединения имеют одинаковую стабильность ^*). Однако в приближении Хюккеля получается, что только анион циклопентадиенила будет иметь электронную конфигурацию с замкнутой оболочкой, и экспериментально найдено, что это единственная стабильная форма пятичленного кольца (например, диметилциклопентадиендикарбоксилат образует стабильный анион I в водной щелочи). Подобно этому семичленное кольцо образует стабильный катион II - катион тропилия

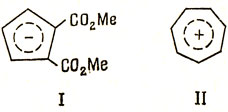
^*) (Было найдено, что, когда взаимодействие между этими структурами учитывается детально, метод ВС приводит к тому же результату, что и приближение Хюккеля [26].)

Однако следует подчеркнуть, что ни один из этих ионов не обнаруживает химических свойств, характерных для бензола, поэтому не очень обоснованно относить их к ароматическим углеводородам. С другой стороны, ферроцен III (см. разд. 18.4) и трополон IV, которые можно рассматривать как производные от этих ионов, вполне можно назвать ароматическими соединениями, потому что они обладают многими характерными для бензола химическими свойствами.

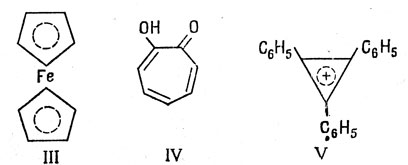
Катион циклопропенила с двумя π-электронами (n = 0) представляет собой до некоторой степени сходный пример. Производные этого иона (как, например, соединение V) относительно стабильны, в то время как производные соответствующего аниона или радикала нестабильны.

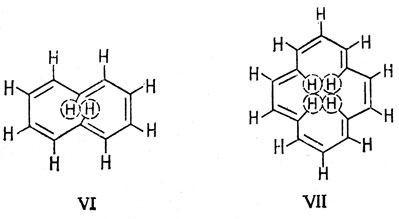
Интересно рассмотреть, что будет при n > 1. Такие соединения известны как аннулены. Более детальное теоретическое рассмотрение показывает, что в больших кольцах альтернирование длин связей С - С, вероятно, имеет место даже в том случае, если число π-электронов равно (4n + 2) (см. [50]). Если n не велико, молекулы не могут иметь плоскую структуру, необходимую для π-электронной стабилизации, из-за возникновения напряжения и отталкивания несвязанных атомов. Так, молекулы С₁₀Н₁₀ (VI) еще синтезированы, а молекула (С₁₄Н₁₄) (VII), хотя и существует, очень нестабильна.

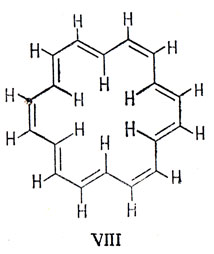
Была приготовлена циклическая система VIII, содержащая 18 атомов углерода (n = 4), которая оказалась более стабильной, чем аннулен, содержащий 20 атомов углерода. Она участвует при довольно специфических условиях в характерных для ароматических соединений реакциях замещения. Однако она стабильна не в том смысле, как бензол, а, вероятно, в силу отталкивания между атомами водорода во внутреннем кольце.

Метод Хюккеля позволяет предсказать, что основное состояние квадратной молекулы циклобутадиена С₄Н₄ должно быть триплетным и существующие экспериментальные данные подтверждают эту точку зрения, так как все попытки получить его простые производные приводят к димерам. На основе самого грубого подхода, основанного на методе ВС, можно предположить, что молекула должна быть стабильна, потому что она представляется двумя эквивалентными схемами, как и бензол. Циклооктатетраен также мог бы иметь триплетное основное состояние, если бы молекула была плоской, но он существует не в виде плоской молекулы и обладает свойствами олефинов. Ее двухзарядный отрицательный ион С₈H₈^2-, однако, включает систему делокализованных π-электронов и, вероятно, имеет плоскую конфигурацию.

Наиболее убедительным доказательством делокализации π-электронов в циклических молекулах является их высокий диамагнетизм. При наличии магнитного поля, перпендикулярного к плоскости молекулы, π-электроны циркулируют как свободные электроны в сверхпроводящем кольце. Это создает магнитное поле противоположного внешнему направлению и приводит к диамагнетизму. Последний ясно обнаруживается в ядерном магнитном резонансе в виде сильного магнитного антиэкранирования протонов внешнего кольца и сильного экранирования протонов внутреннего кольца. Однако следует еще раз подчеркнуть, что наличие такого физического свойства само по себе не может служить достаточным основанием для того, чтобы молекулу можно было считать ароматической.