15.7. Гетероатомные молекулы

До сих пор при обсуждении приближения Хюккеля рассматривались только системы, содержащие атомы углерода. Введение атома азота или кислорода в ненасыщенную систему требует новых значений кулоновских и резонансных интегралов. Изменения интегралов α и β обычно выражаются через значения α_С и β_С-С этих интегралов для молекулы бензола как стандарта следующим образом:

Трудно получить определенные значения для параметров h_X и k_C-X, потому что, как видно из следующего раздела, параметры Хюккеля зависят от того, какого рода экспериментальные данные привлекаются для их оценки. Приближенные значения h_X можно считать известными, так как величина α_Х должна быть связана с электроотрицательностью атома X. Принимают, что h_X зависит линейно от разности электроотрицательностей атомов X и С. Следует, однако, различать такие случаи, как, например, атом азота в пиридине, где он дает один π-электрон в систему π-электронов, и атом азота в пирроле, где отдается два электрона. В общем приемлемы следующие значения [78]:

Когда значения h_X и k_C-X выбраны, вычисление орбитальных коэффициентов производится, как и раньше. Например, для молекулы формальдегида Н₂С = 0 вековое уравнение имеет вид

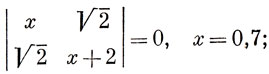
что дает Е₁ = α + 2,7β, Е₂ = α - 0,7β. Связывающая МО близка по энергии к АО кислорода, а разрыхляющая МО - к АО углерода. Это показано на рис. 15.5.

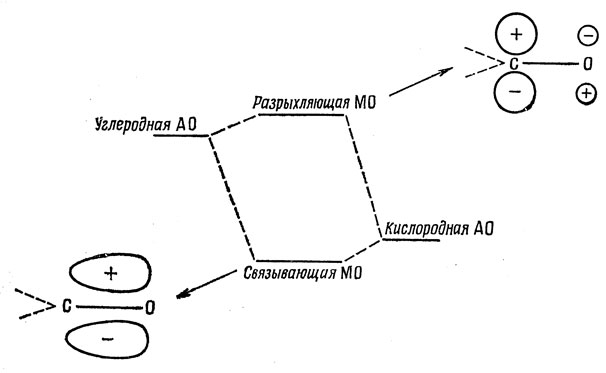
Рис. 15.5. Хюккелевские орбитали карбонильной группы

Другой метод решения подобного рода задач состоит в том, что введение гетероатома рассматривается как возмущение МО и энергий изоэлектронного углеводорода. Так, МО формальдегида при таком подходе можно представить в виде линейной комбинации МО этилена. Таким способом получены некоторые полезные выражения, характеризующие изменения электронной плотности при гетерозамещении.

Из выражения (15.12) можно найти выражение для полного дифференциала энергии ε:

Однако изменение q_μ и p_μν при постоянных α_μ и β_μν не вносит вклада в dε, так как орбитальные энергии были вычислены методом, основанным на вариационном принципе, т. е. ε уже представляет собой минимум по отношению к вариации коэффициентов с_rμ и, следовательно, к вариации q_μ и p_μν. Поэтому из выражения (15.31) следует что,

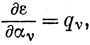
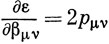
и далее

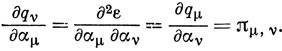
Таким образом, изменение величины α_μ вносит такое же возмущение в π-электронный заряд на атоме с номером ν, как аналогичное изменение α_ν в π-электронный заряд на атоме μ. Производная

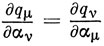
называется взаимной поляризуемостью атомов μ и ν и обозначается символом π_μ,ν [16]. Можно также поставить вопрос, как влияет на величину q_ν изменение резонансного интеграла β_μπ.

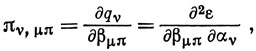
Величину π_ν,μπ называют взаимной поляризуемостью атом - связь. Далее, можно задаться вопросом, как изменяются порядки связей при изменении α и β.

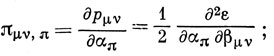
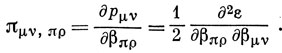
Эти величины называются взаимными поляризуемостями связь - атом и связь - связь соответственно. Наиболее важной среди всех введенных здесь величин является π_μ,ν. Выражение для нее можно получить в первом порядке теории возмущений (6.52) (см. задачу 15.4):

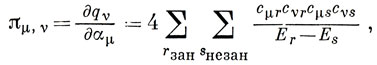
где суммирование проводится по всем занятым и незанятым орбиталям соответственно. Можно доказать, что для альтернантных углеводородов π_μ,ν положительно, если атомы с номерами μ и ν относятся к одному набору, и отрицательно - если к разным. Иначе говоря, для альтернантных углеводородов π_μ,ν положительно или отрицательно в зависимости от того, разделены атомы нечетным или четным числом связей. В нейтральных альтернантных углеводородах все π-заряды на атомах равны единице. Поэтому если один атом углерода замещается на гетероатом X (с кулоновским интегралом α_Х), то в в первом порядке теории возмущений измененные значения q_ν равны

Взаимные поляризуемости в молекуле бензола (в единицах β^-1) таковы: орто (π_{1, 2} = - 17/108; мета (π_{1, 3}) = + 1/108 и пара (π_{1, 4}) = - 11/108; самополяризуемость (π_{1, 1}) = + 43/108. Пусть нас интересуют заряды на атомах в молекуле пиридина. Тогда, полагая (αN - α_C) = 0,5β, получаем следующий результат:

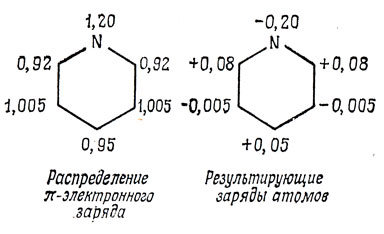
При таком рассмотрении предполагалось, что гетерозамещение приводит к изменению только одного кулоновского интеграла. Изменения кулоновских интегралов атомов, соседних с гетероатомом, и резонансных интегралов для связанных с ним атомов оказывает гораздо меньшее влияние на распределение электронной плотности.