15.8. Критика метода Хюккеля

В гл. 12 были рассмотрены приближения, присущие методу МО. Метод Хюккеля, помимо этих, содержит ряд дальнейших приближений, приемлемость которых, по-видимому, весьма сомнительна. До какой степени можно оправдать эти приближения? ^*)

^*) (Метод Хюккеля получает более строгое обоснование в теории, учитывающей взаимодействие электронов [см. Веселов М. Г., Местечкин М. М., Литовский Физ. Сб., 3, 269 (1963); Flscher-Hjalmars I., J. Ghem. Phys., 42, 1962 (1965)]. - Прим. ред.)

Прежде всего метод Хюккеля практически полезен потому, что не ставит перед собой слишком далеко идущих целей. Метод Хюккеля не применяется для последовательного теоретического вычисления каких-либо отдельных величин; он лишь позволяет установить связь одних экспериментальных данных с другими. Вычисляемые энергии, электронные плотности и другие величины выражены через энергетические параметры α и β. Формально эти параметры определены как интегралы, содержащие гамильтониан Н, однако связь этого гамильтониана с полным гамильтонианом не конкретизируется.

Если в молекуле нет гетероатомов, то все относительные энергии в приближении Хюккеля выражаются через один параметр β. Это означает, что должно существовать линейное соотношение между экспериментальными значениями энергии и энергиями Хюккеля, а тангенс угла наклона соответствующей прямой определяется значением β. Это показано на рис. 15.6, где на графике отложена частота первой интенсивной электронной полосы поглощения в ароматических углеводородах, образованных конденсированными бензольными кольцами (нафталин, пирен), в зависимости от энергии, необходимой для возбуждения электрона с высшей занятой МО ψ₁ (высшей связывающей МО) на низшую вакантную (разрыхляющую) орбиталь ψ_-1 в единицах β. Прямая, проведенная так, чтобы экспериментальные точки были по возможности близки к ней, удовлетворяет уравнению [33]

Прямая не проходит через начало координат и показывает, что энергия возбуждения превышает значение, вычисленное по Хюккелю. Все же, если имеется соединение, спектр которого не известен, можно предсказать положение полосы поглощения с точностью ±1500 см^-1 и с предельной вероятностью 95%. Значение β, наилучшим образом отвечающее экспериментальным данным, равно -21900 см^-1, что соответствует энергии -2,71 эв.

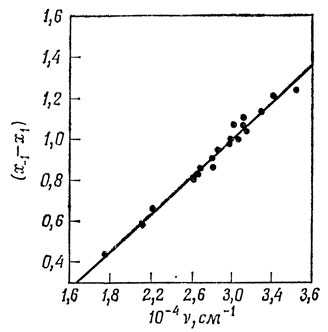
Рис. 15.6. Корреляция между частотой первой интенсивной электронной полосы поглощения и первой хюккелевской энергией возбуждения

В качестве второго примера возьмем полярографические потенциалы полуволны (ε_1/2) для пятидесяти ароматических углеводородов (гораздо более широкий класс молекул, чем на рис. 15.6, в частности включающий азулен и дифенил). Эти потенциалы можно связать с энергией, выделяющейся при присоединении электрона к углеводороду и, таким образом, с хюккелевской энергией низшей вакантной орбитали ψ_-1. В этом случае уравнение прямой имеет вид [78]

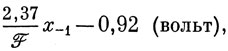
где F - постоянная Фарадея. Тангенс угла наклона этой прямой определяет величину β в электронвольтах: β = - 2,37 эв.

Наконец, рассмотрим корреляцию между хюккелевской энегией делокализации E_D (т. е. полная хюккелевская энергия за вычетом 2β на каждую формальную двойную связь) и наблюдаемыми значениями энергии делокализации (энергии резонанса). В качестве последней обычно принимают разность между теплотой сгорания углеводорода и той теплотой сгорания, которая вычисляется на основе предположения об аддитивности энергий связи [45] (например, 54,0 ккал для каждой связи С - Н; 49,3 ккал для каждой связи С - С; 121,2 кал для каждой связи С = С и т. д.). Корреляция для тех же соединений, что и на рис. 15.6, показана на рис. 15.8, а уравнение изображенной там прямой имеет вид

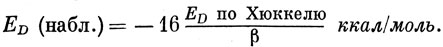
Тогда наблюдаемые значения получаются при β = - 16 ккал/моль, или - 0,69 эв.

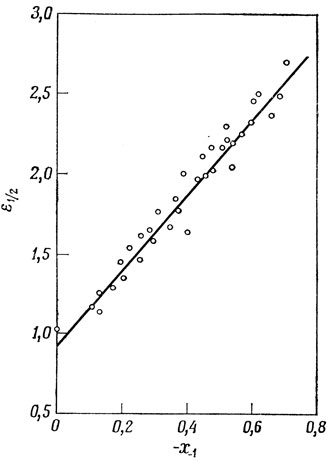
Рис. 15.7. Корелляция между полярографическим потенциалом полуволны и хюккелевской энергией низшей вакантной орбитали

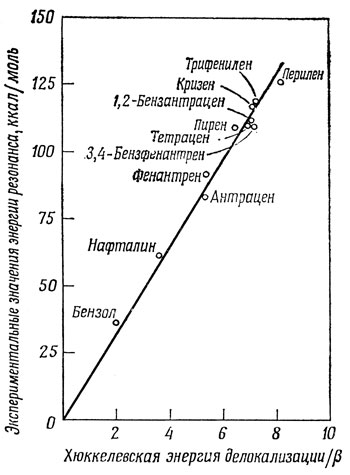
Рис. 15.8. Корелляция между наблюдаемой энергией резонанса и хюккелевской энергией делокализации

Три приведенных выше примера показывают, что линейное соотношение между хюккелевскими энергиями и рассмотренными свойствами довольно хорошо выполняется. Однако значения β, получающиеся во всех трех случаях, довольно сильно различаются; в частности, абсолютные значения β, дающие наилучшую энергию делокализации, много меньше тех, которые приводят к наилучшим значениям восстановительного потенциала или энергии возбуждения. Причина этого расхождения заключается в следующем: для вычисления энергии нужно использовать полный гамильтониан молекул, а не одноэлектронный псевдогамильтониан метода Хюккеля. Если это учесть, то оказывается, что такие величины, как энергии возбуждения, сродство к электрону и энергии диссоциации, выражаются не только через одни электронные интегралы типа β и β, но зависят также от интегралов, описывающих межэлектронное взаимодействие (см. разд. 10.7). Принимая β как электрический параметр, можно в некоторых случаях (но не всегда) компенсировать пренебрежение этими интегралами. Но теперь при описании различных свойств молекул β представляет собою различные комбинации интегралов, и потому значения β, приводящие к согласию вычислений с экспериментальными данными в одном случае, могут отличаться от значений, являющихся наиболее подходящими для результатов экспериментов в другом случае ^*).

^*) (Различие численных значений параметров α и β, получаемых из разных опытных данных, получило количественное объяснение в теории, учитывающей электронное взаимодействие [см. Местечкин М. М., ЖФХ, 35, 431 (1961)]. - Прим. ред.)

Именно поэтому не существует единых для всех молекул с гетероатомами значений параметров аир. Значение aN, при котором лучше всего описывается основность содержащих азот гетероциклических молекул, не обязательно является наилучшим для предсказания плотности неспаренного электрона в азотсодержащих радикалах, потому что aN при вычислении этих двух характеристик молекул выражает различные комбинации одно- и двухэлектронных интегралов.

Имеется несколько случаев, даже среди сопряженных углеводородов, в которых метод Хюккеля в его простейшей форме дает довольно плохие результаты. Например, частота возбуждения молекулы бутадиена, вычисленная по формуле (15.38), составляет 35300 см^-1, а экспериментальное значение равно 46100 см^-1. Причина расхождения состоит в том, что не все длины связей в молекуле бутадиена одинаковы, а потому использование одного и того же значения β для всех связей является грубым приближением. Хотя параметр β не достаточно хорошо определен как величина, все же ясно, что он должен быть приближенно связан с перекрыванием включенных в связь двух АО и с увеличением длины связи уменьшается приблизительно экспоненциально.

Для молекул, где имеет место сильное альтернирование связей, как, например, в сопряженных полиенах, существенно, чтобы зависимость β от длины связи была учтена. Если, например, взять для коротких (двойных) связей β = - 4,00 эв и для длинных (простых) связей β = - 2,88 эв, то получается очень хорошее согласие между наблюдаемым и вычисленным положением первой полосы поглощения в этих соединениях, как можно видеть из рис. 15.9.

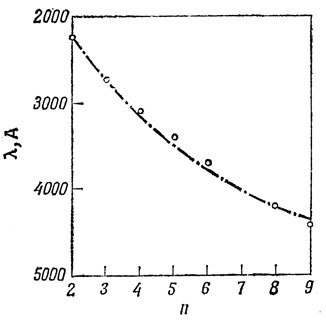
Рис. 15.9. Корреляция между положением первой электронной полосы поглощения линейных полиенов, имеющих n двойных связей, и первой хюккелевской энергией возбуждения при наличии альтернирования длин связей

Другой случай, когда нужно учитывать изменение β, представляют молекулы, в которых участвующие в сопряжении атомы углерода не лежат в одной плоскости. Например, эксперимент показывает, что дифенил (в растворе или в газовой фазе), - не плоская молекула вследствие стерического взаимодействия между атомами водорода, находящимися в орто-положениях по отношению к центральной связи. Если θ - угол между плоскостями двух бензольных колец, то можно считать, что β для центральной связи изменяется как cos θ; когда два кольца перпендикулярны друг другу, то β = 0 и в методе Хюккеля получаются две независимые сопряженные системы.

Метод Хюккеля дает для альтернантных углеводородов значительно лучшие результаты, чем для неальтернантных. Например, дипольный момент молекулы азулена при расчете по Хюккелю оказывается равным 7D, тогда как экспериментальное значение составляет приблизительно 1D. Причина такого расхождения заключается в том, что, хотя α_μ в приближении Хюккеля характеризует электронную орбитальную энергию для орбитали φ_μ, взаимодействие этого электрона с другими π-электронами в молекуле не учитывается. Ясно, что увеличение электронного заряда на атоме μ должно обусловливать положительную добавку к величине α_μ.

Простейший способ учета влияния электронной плотности молекулы на α_μ дает формула Уэйленда - Манна

где q_μ - π-электронный заряд, вычисленный по формуле (15.8). Если он равен 1, как, например, в нейтральных альтернантных углеводородах, то для α_μ получается стандартное значение α₀. Если заряд q_μ отличен от 1, то, как видно из формулы (15.41), в величину α_μ вносится поправка (1 - q_μ) ω β, где ω - постоянная. Наилучшее согласие с экспериментом получается при ω = 1,4 [78]. Поскольку β отрицательно, то эта поправка положительна, если q_μ больше единицы, и отрицательна при q_μ меньших единицы.

Расчеты по формуле Уэйленда - Манна (иногда их называют ω-техникой), как будет видно, есть первое приближение к расчету по методу ССП, и метод получения орбиталей Уэйленда - Манна следует обычной итерационной процедуре самосогласования. Исходя, например, из орбиталей, полученных в приближении Хюккеля, вычисляют q_μ и затем аи. Найденное значение α_μ используется затем в новом расчете по методу Хюккеля, а на основе полученных при этом орбиталей вычисляется новое значение q_μ. Расчет продолжают до тех пор, пока не будет достигнуто самосогласование.

Расчет Уэйленда - Манна дает для дипольного момента молекулы азулена при ω - 1,4 значение 4,7D, что значительно лучше результата, получаемого в приближении Хюккеля, хотя все еще много больше экспериментального значения.

Наконец, обратимся к наиболее грубому приближению Хюккеля - приближению нулевого перекрывания, когда интегралы перекрывания считают равными нулю даже для АО, центрированных на соседних атомах. При длине связи 1,4 А значение интеграла перекрывания 2pπ-АО соседних атомов равно 0,25, которое, конечно, не является малой величиной. Однако применимость этого приближения основана опять на том, что параметры α и β - не строго определенные величины. Вместо того чтобы считать эти параметры интегралами, содержащими 2pπ-АО, можно с тем же правом рассматривать их как интегралы между ортонормированными АО, определенными из выражений (12.7) и (12.10).

Орбитали, которые входят в определения величин α и β, но без предположения о нулевом перекрывании, называются орбиталями Уэйленда. Если в приближении Хюккеля орбиталь соответствует энергии

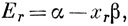
то в приближении Уэйленда она имеет энергию

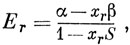
где S - интеграл перекрывания между соседними орбиталями. Кроме того, если хюккелевская орбиталь содержит коэффициенты c_rν, то орбиталь Уэйленда включает коэффициенты (1 - x_rS)^-1/2c_rν.

Однако случаев, когда соответствие между экспериментальными данными и расчетами в приближении Уэйленда, было бы значительно лучше, чем в приближении Хюккеля, не известно. По этой причине в настоящее время мало расчетов выполняется по методу Уэйленда.

Подведем некоторые итоги. Метод Хюккеля есть метод установления связей между экспериментальными данными для классов родственных соединений. Это особенно полезно, когда класс содержит большое число соединений (например, все ароматические углеводороды), а число используемых параметров мало. При переходе к системам, содержащим гетероатомы, как наблюдается, число параметров, которые следует определить на основе эксперимента, быстро растет, и в то же время число молекул в каждом классе становится меньшим. Поэтому параметры, характеризующие гетероатомы, до сих пор твердо не установлены. Параметры метода Хюккеля заменяют собою сложные интегралы, появляющиеся в любом неэмпирическом методе. По этой причине лучшие значения параметров зависят от того, какая экспериментально наблюдаемая характеристика исследуется.

В следующих двух главах мы обсудим применение метода Хюккеля к задачам о химическом равновесии и реакционной способности, но сначала кратко остановимся на более точном варианте электронного приближения, в котором межэлектронное отталкивание рассматривается в явном виде.