15.9. Учет взаимодействия электронов в π-электронном приближении

Метод Хюккеля не рассматривает взаимодействия электронов, хотя и предполагается, что хюккелевский гамильтониан содержит некоторое усредненное межэлектронное взаимодействие. Метод Уэйленда - Манна учитывает его в весьма грубой форме путем предположения о зависимости кулоновского интеграла от величины заря да на исследуемом атоме. Более последовательное рассмотрение (будем называть его методом ППП) было предложено Паризером, Парром и Поплом ^*). Характерным для него является учет взаимодействия электронов в приближении нулевого перекрывания ^**).

^*) (Более полное описание метода ППП имеется в книге [62].)

^**) (Такое приближение часто называют приближением нулевого дифференциального перекрывания и обозначают НДП. - Прим. перев.)

При расчете энергии с волновой функцией, построенной в приближении МО ЛКАО, и при использовании полного гамильтониана появляются интегралы межэлектронного отталкивания следующего вида:

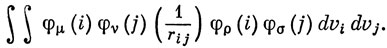
С физической точки зрения этот интеграл описывает взаимодействие зарядов, распределенных с плотностями φ_μφ_ρ (i) и φ_νφ_σ (j). В методе Хюккеля пренебрегают перекрыванием двух орбиталей, относящихся к различным атомам; поэтому в приближении нулевого перекрывания с этим согласуется пренебрежение всеми двухэлектронными интегралами, зависящими от плотности перекрывания. Таким образом, остаются лишь интегралы вида

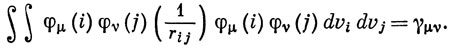
Это упрощение, по существу, вытекает из предложенного ранее Малликеном приближенного способа вычисления интегралов:

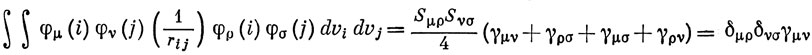
(в приближении нулевого перекрывания).

Метод Хюккеля построен на использовании параметров α и β, представляющих собой интегралы, которые содержат не определенный в явном виде одноэлектронный гамильтониан. Аналогичные параметры используются и в методе ППП, но здесь они хорошо определены; их называют интегралами остова [см уравнение (10.58)]:

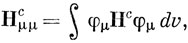
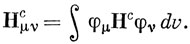
Н^с содержит члены, которые зависят от координат одного электрона, например электрона с номером 1: оператор кинетической энергии и потенциал поля, создаваемого σ-остовом углеводородной молекулы. Этот потенциал можно представить в виде суммы слагаемых V_ρ, относящихся к отдельным атомам углерода, т. е.

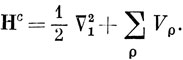
Теперь гамильтониан Н^с будет различным для разных молекул, и потенциал вблизи атома будет зависеть от его положения в молекуле. Поэтому ясно, что величины H_μμ^c и H_μν^c нельзя считать, как это делается в методе Хюккеля, одинаковыми для всех атомов углерода и всех связей С - С. Если подставить соотношение (15.47) в выражение (15.46), можно получить

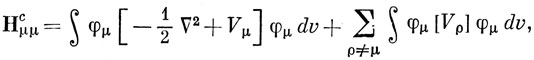
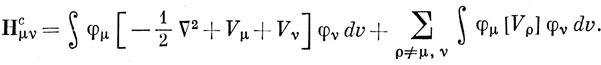
Первый член в выражении (15.48) можно считать одинаковым для всех атомов данного типа. Грубо говоря, он равен взятому со знаком минус потенциалу ионизации I_μ, соответствующему удалению электрона с 2р-орбитали при валентном состоянии. Аналогично первый член в H_μν^c можно считать постоянным для одних и тех же пар атомов при одинаковых длинах связей между ними. Членами, содержащими V_ρ, нельзя пренебрегать. Предположим, что энергия электрона, распределенного с плотностью φ_μ² в поле ρ-го атомного остова (ρ ≠ μ) с зарядом Z_ρ, равна по величине и противоположна по знаку энергии того же электрона в поле заряда, распределенного с плотностью Z_ρφ_ρ². Тогда можно утверждать, что

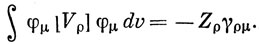
Аналогично

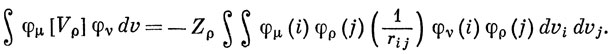
Такими двухэлектронными интегралами пренебрегают в приближении нулевого перекрывания [см. выражение (15.44)]. Отсюда следует, что в методе ППП H_μν^c - параметр, который можно считать постоянным подобно интегралу β в методе Хюккеля. Однако Н_μμ^c отличается от хюккелевского параметра α_μ, так как эта величина изменяется от атома к атому в соответствии с выражением

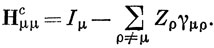
Для вычисления энергии с многоэлектронной волновой функцией, построенной из ортогональных спин-орбиталей, можно воспользоваться соотношениями типа (10.63) и (10.79) и построить МО в приближении ЛКАО. В общем случае это приводит к очень сложным уравнениям, но в приближении ППП задача несколько упрощается. Это можно понять, рассматривая выражения, входящие в уравнения Рутана (10.83):

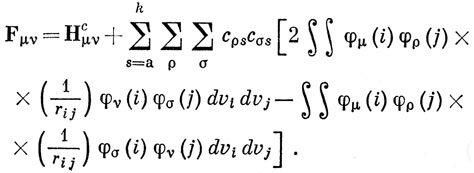
При μ = ν в приближении нулевого перекрывания получим

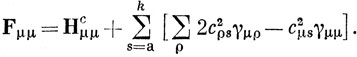
Это выражение можно упростить, вводя заряды на атомах [см. соотношение (15.8)] и учитывая выражение (15.52):

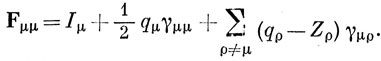
В случае μ ≠ ν имеем

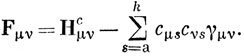
Используя определение порядка связи [см. выражение (15.9)], получим

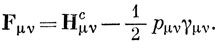
При таком определении интегралов F сравнительно легко вычислить энергию с любой волновой функцией или получить из выражений (10.84) самосогласованные орбитали.

Для нейтральных альтернантных углеводородов можно показать, что свойство парности МО, которое является существенной особенностью метода Хюккеля, сохраняется, если самосогласованные орбитали определяются на основе приведенных выше выражений для интегралов F_μν. Аналогично сохраняется также равномерное распределение электронного заряда между атомами, и в этих случаях выражение (15.55) приводит к выражению

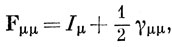
которое можно рассматривать как постоянную, аналогичную α в методе Хюккеля. Поправки Уэйленда - Манна для молекул, где электронная плотность неоднородна, дают грубое приближение к уравнению (15.55), в котором пренебрегают действием разделенных зарядов (γ_μν = 0, μ ≠ ν), а ωβ эквивалентно

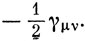
Метод ППП в том виде, в каком он сейчас используется, представляет собой полуэмпирический подход, в котором параметры H_μν^c и γ_μν выбираются так, чтобы получить согласие с экспериментальными данными. Поскольку в методе ППП используется большее число параметров, чем в приближении Хюккеля, было бы удивительно, если бы согласие с экспериментом не улучшилось. Однако метод ППП обладает некоторыми существенными достоинствами. Во-первых, параметры H_μν^c в отличие от β не меняются при переходе от изучения одного свойства к изучению другого. Во-вторых, существуют некоторые экспериментальные результаты, которые невозможно объяснить в приближении Хюккеля, потому что они представляют прямые следствия взаимодействия электронов. Наиболее важными среди таких свойств являются многие характеристики электронных спектров. Например, разница энергий синглетного и триплетного состояний молекулы определяется интегралами межэлектронного взаимодействия (выражаемого членами γ в методе ППП), как было показано на примере атома гелия (разд. 9.5). Таким образом, метод ППП представляет собой очень полезное расширение эмпирических методов расчета ненасыщенных углеводородов.