15.10. Модель свободных электронов для молекул, содержащих π-электроны

Главной особенностью π-электронов является их делокализация. Простейшей моделью, в которой учитывается это свойство, является модель свободных электронов. По существу, при этом игнорируют тонкие детали потенциала, создаваемого электронами и ядрами в молекуле, и просто полагают, что электроны находятся в некотором объеме с постоянным потенциалом; размеры объема определяются размерами молекулы. Проиллюстрируем это на простом примере линейного полнена.

Рассмотрим линейный полиен, содержащий 2n атомов углерода. π-электроны делокализованы вдоль цепочки, и основные черты задачи выявляются при обсуждении одномерного потенциала. Длина полиеновой цепочки с добавлением по одной длине связи за крайними атомами принимается за длину потенциального ящика (иногда добавляется только по половине длины связи, но эта деталь несущественна). Поэтому МО и соответствующие им энергии можно определить, если подставить длину ящика а = (2n + 1) d, где d - длина связи, в решения задач (2.4) - (2.7) о частице в потенциальном ящике:

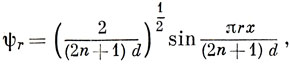
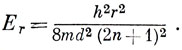
На рис. 15.10. показан вид первых четырех МО для бутадиена в модели свободных электронов. Существует большое сходство между этими МО и соответствующими хюккелевскими орбиталями, приведенными на стр. 352. Функция ψ₁ - безузловая; функции ψ₂ соответствует узел на центральной связи; ψ₃ обладает двумя узлами, a ψ₄ имеет узлы на каждой связи. Сходство хюккелевских орбиталей с МО, полученными в модели свободных электронов, распространяется также на сопряженные цепочки с ответвлениями и ароматические молекулы. Амплитуды орбиталей модели свободных электронов аналогичны соответствующим хюккелевским коэффициентам.

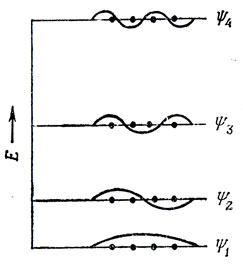
Рис. 15.10. Молекулярные орбитали бутадиена в модели свободных электронов

Модель свободных электронов довольно широко использовалась для интерпретации электронных спектров ненасыщенных углеводородов. Привлекательной чертой модели является то, что в отличие от приближения Хюккеля в вычисленные значения энергии не входят никакие эмпирические параметры ^*). Например, в основном состоянии молекула бутадиена имеет конфигурацию ψ₁²ψ₂², в первом возбужденном - конфигурацию ψ₁²ψ₂ψ₃. Поэтому энергия перехода равна

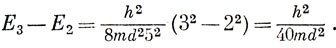
Беря длину связи С - С равной 1,4 А, получим

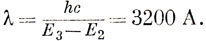
Экспериментальное значение составляет 2200 А.

^*) (Если не считать значения длины связи d. - Прим. перев.)

Если принять во внимание чрезвычайную грубость модели свободных электронов, то представляется неожиданным столь близкое согласие полученного результата с экспериментальным. Линейные полиены на самом деле не являются удачными объектами для проверки метода; альтернирование длинных и коротких связей означает, что электроны нельзя считать полностью делокализованными вдоль всей молекулы. Как уже было указано раньше, в приближении Хюккеля для таких молекул также получаются плохие результаты, если не учитывать для длинных и коротких связей различные значения β.

Были исследованы видоизменения модели свободных электронов, в которых постоянный потенциал модулируется некоторым возмущением, учитывающим альтернирование длин связей. Однако эти видоизменения имеют тот недостаток, что в этом случае уравнение Шредингера можно решить только численно и по необходимости модулированные потенциалы содержат некоторые неизвестные постоянные. Сегодня модель свободных электронов рассматривается как интересная попытка освещения природы π-электронных молекул, но практически метод Хюккеля проще и, основываясь на нем, легче учитывать межэлектронное взаимодействие.

Стендовый моделизм диорамы купить диорама на фронт стендовый моделизм.