16.3. Резонансные эффекты

Наибольшим успехом электронной теории органической химии было объяснение механизма переноса электронных пар от одной группы к другой по цепи напряжения. Например, на языке ВС основное состояние молекулы

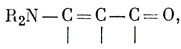
можно было бы представить структурами

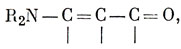
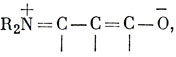
возможно, с добавлением структур, таких, как

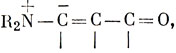
которые могут оказаться существенными. Структуры такого типа, согласующиеся с основными положениями органической химии, такими, как четырехвалентность углерода, называют каноническими. В теории "резонанса" молекула описывается ее главными каноническими структурами, с применением следующей символики:

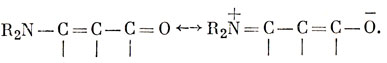
Таким способом химик-органик обозначает, что электронодонорная группа R₂N оказывает заметное влияние на свойства электроноакцепторной группы С = О. Используется и другой способ представления:

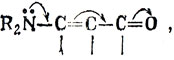
который, однако, применяют также, чтобы показать полное перераспределение электронных пар в реакции, и, вероятно, лучше использовать его только в этом смысле.

Ингольд четко разграничивал поляризацию в основном состоянии, которую он называл мезомерным эффектом (обозначая буквой М), и возможную поляризацию в переходном состоянии, названную им электромерным эффектом (Е). Суммарный результат действия этих двух эффектов Ингольд назвал таутомерным эффектом, однако это очень неудачный термин, так как в настоящее время четко выявлена разница между таутомерией и резонансом. Поэтому будем пользоваться термином резонансный эффект (R) как для эффекта М, так и для эффекта Е, хотя и считаем очень важным проводить различие между поляризацией в основном состоянии и возможной поляризацией в молекуле в процессе реакции, но это различие относится лишь к степени, а не к характеру поляризации.

При обсуждении резонансного эффекта мы коснулись вопроса о взаимодействии π-орбиталей заместителя с π-МО остатка. В молекуле стирола, например, взаимодействие с π-орбиталями винильной группы ведет к понижению электронной энергии молекулы. Полная хюккелевская энергия стирола меньше, чем энергия молекул бензола и этилена в отдельности на величину - 0,42β.

Поскольку стирол является альтернантным углеводородом, заряды на его атомах одинаковы, т. е. не происходит переноса заряда между винильной группой и кольцом. Однако в более общем случае замещающие группы, содержащие π-электроны, можно классифицировать либо как доноры (+R), либо как акцепторы (-R) π-электронов. Заместитель будет донором, если он содержит заполненные π-орбитали, имеющие относительно малый потенциал ионизации. При наличии же вакантных π-орбиталей с относительно большим сродством к электрону заместитель будет акцептором электронов.

Все группы +R содержат неподеленные пары электронов, волновая функция которых обладает π-симметрией (т. е. антисимметрична по отношению к отражению в плоскости сопряженной системы). В табл. 16.2 наиболее часто встречающиеся группы расположены в порядке возрастания их донорных свойств, определяемых по величине потенциала ионизации, и оказывается, что этот порядок в общем совпадает с тем, который установлен на основании химических данных.

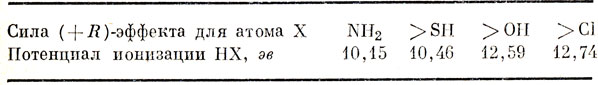
Таблица 16.2. Донорные (+R) группы

Все обычные акцепторы представляют собою ненасыщенные группы и содержат незанятые электронами низколежащие разрыхляющие π-орбитали. Сродство к электрону очень трудно измерить экспериментально, и поэтому невозможно составить таблицу, подобную табл. 16.2. Из спектроскопических данных можно получить грубую оценку (-R)-эффекта (табл. 16.3).

Таблица 16.3. Акцепторные (-R) группы

Заместитель, подобный SH, может обладать акцепторными свойствами благодаря наличию вакантных 3d-орбиталей, хотя в общем он ведет себя, как донор. Аналогично карбонильная группа может отдавать электроны со своей связывающей МО, но в общем ведет себя, как акцептор.

Рассмотрим метилвиниловый эфир (I) и метилакрилат (II) как примеры замещенных этиленов (+R)- и (-R)-группами. Химик-органик изобразит свойства этих групп следующим образом:

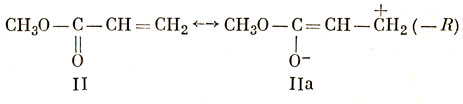
Если пытаться произвести расчет этих молекул в приближении Хюккеля, то нужно включить значения кулоновского и резонансного интегралов для гетероатома и учесть также индуктивный эффект. Для того чтобы изучить отдельно резонансный эффект, целесообразно сначала рассмотреть аллильный анион (СН‾₂ - СН = СН₂) и аллильный катион (СН⁺₂ - СН = СН₂) как модели (+R)- и (-R)-систем соответственно.

Уравнения для орбитальных коэффициентов, написанные в приближении Хюккеля для аллильной системы, имеют вид

Решив эти уравнения, получим следующие хюккелевские орбитали:

ψ1 = 1/2 φ1 + √1/2 φ2 + 1/2 φ3    E1 = α + √2β

ψ2 = √1/2 φ1 - √1/2 φ2 + 1/2 φ3   E2 = α

ψ3 = 1/2 φ1 - √1/2 φ2 + 1/2 φ3    E1 = α - √2β.

В аллильном катионе два π-электрона находятся на орбитали ψ₁, а в анионе два электрона занимают орбиталь ψ₁ и два - орбиталь ψ₂. Вычисленные результирующие заряды на атомах таковы:

Эти результаты согласуются с картиной валентных схем, где катион, например, представляется как смесь следующих структур:

Приведенные выше результаты можно получить и не производя расчетов по методу Хюккеля, так как вычисленное распределение зарядов как раз то, которое получится, если взять нейтральный альтернантный углеводород (аллильный радикал), в котором заряды распределены равномерно (стр. 355), и добавить или удалить электрон с орбитали ψ₂. На основании того, что аллил - альтернантный углеводород, его орбитали должны удовлетворять общей теореме парности, доказанной на стр. 356, т. е. если имеется орбиталь с энергией α + x_rβ, то должна быть и орбиталь с энергией α - х_rβ. Число получаемых МО равно числу АО, включенных в линейную комбинацию, и поэтому для альтернантных углеводородов с нечетным числом атомов, участвующих в сопряжении, должна быть одна МО с энергией Е = α (х = 0). Ее называют несвязывающей орбиталью.

Если вернуться теперь к системе уравнений (15.5) для орбитальных коэффициентов в методе Хюккеля

то можно увидеть, что в случае х = 0 сумма коэффициентов соответствующей орбитали, относящихся к АО соседей любого из атомов, равна нулю. Поскольку с помеченными атомами непосредственно связаны лишь непомеченные, то равны нулю все коэффициенты, характеризующие либо помеченные, либо непомеченные атомы. Легко видеть, что коэффициенты, относящиеся к набору с меньшим числом атомов, который условились считать непомеченным, равны нулю. Покажем теперь, что, используя это свойство, очень легко получить коэффициенты несвязывающей орбитали любого нечетного альтернантного углеводорода.

В качестве примера возьмем пентадиенил

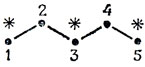
Если взять сумму коэффициентов АО атомов, соседних с атомом 1, то сразу получаем с₂ = 0, в согласии с тем, что нулевые коэффициенты присущи АО непомеченных атомов. Пусть теперь с₁ = а. Переходя к соседям атома 2, получим с₃ = - а, суммирование же коэффициентов по АО, соседних с атомом 4, дает с₅ = а. Таким образом, несвязывающая орбиталь имеет следующие коэффициенты:

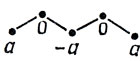
Для нормировки необходимо, чтобы 3а² = 1, откуда а = √1/3. Поэтому при добавлении одного электрона на несвязывающую МО нейтрального радикала получаем следующую картину распределения результирующих зарядов на атоме аниона:

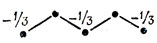
Эта процедура, впервые предложенная Лонге-Хиггинсом, дает очень простой способ выяснения того, как влияет R-замещение на электронную плотность в альтернантном углеводороде. Сначала рассмотрим эффект введения в положение заместителя группы СН₂. При этом получается нечетный альтернантный углеводород, в котором атом углерода группы СН₂ относится к помеченному набору, и коэффициенты несвязывающей МО можно вычислить по методу, изложенному выше. Для получения моделей (+R)- и (-R)-замещения добавим или удалим соответственно электрон с несвязывающей орбитали и воспользуемся ее коэффициентами для определения электронных зарядов. Таким образом, можно рассматривать анион пентадиенил а, обсуждавшийся выше, как модель, описывающую влияние (+R)-группы, присоединенной к молекуле бутадиена (например, МеО - СН = CH - СН = СН₂).

Электронная теория органической химии особенно успешно объяснила качественно ориентирующее действие замещающих групп в ароматических соединениях. Присоединение (+R)-группы к молекуле бензола увеличивает электронную плотность в орто- и пара-положениях, а присоединение (-R)-группы уменьшает электронную плотность в этих положениях (связь этих свойств с реакционной способностью будет рассмотрена в следующей главе). В теории резонанса это изображают посредством следующих канонических форм:

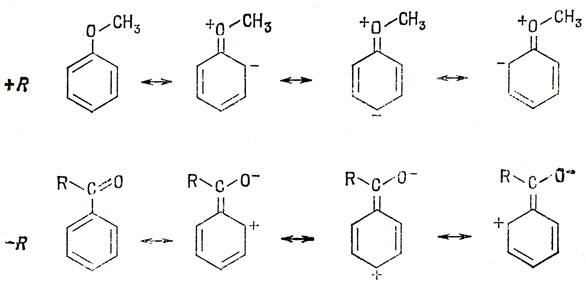
Электронная плотность в мета-положении не изменяется, если полагать, что структуры, содержащие длинные связи, такие, как структура I, несущественны:

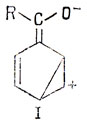
Метод Хюккеля приводит к тому же результату. Следуя данному выше способу определения коэффициентов связывающей МО, получим для бензильного радикала следующий результат:

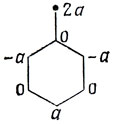
Из условия нормировки имеем 7а² = 1. Таким образом, находим распределение заряда в бензильном анионе (модель анизола) и в бензильном катионе (модель ацетофенона), которое показывает, как изменяются заряды в орто- и пара-положениях.

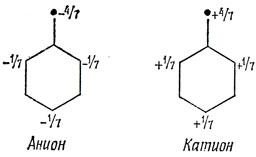
В рассмотренном примере метод Хюккеля и теория резонанса согласуются, если предположить, что в теории резонанса три ионные структуры имеют одинаковые веса. Это соответствие имеет место и для других молекул, содержащих шестичленные кольца, но для альтернантных углеводородов, содержащих четырехчленные кольца, результаты обоих методов не всегда согласуются и, как видно из следующей главы, метод Хюккеля находится в лучшем согласии с экспериментом.

Пока что в качестве заместителя была рассмотрена лишь метиленовая группа, причем СН₂^- изображал (+R)-группы, а СН₂⁺ представлял (-R)-группы. На самом деле различные группы обладают неодинаковой донорной или акцепторной способностью. Для того чтобы подробнее ознакомиться с этой проблемой, рассмотрим три класса резонирующих заместителей: типа бензильного аниона, стирола и 2-фенилпропенильного аниона:

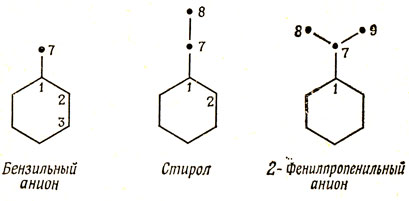
Бензильный анион представляет собой сопряженную систему, изоэлектронную таким молекулам, как фенол, анизол, анилин и т. д. Для проведения расчета этих молекул по методу Хюккеля нужно задать значения кулоновского интеграла гетероатома (α₇) и резонансного интеграла β_1-7. Кроме того, если связь 1-7 достаточно полярна, она будет влиять на кулоновский интеграл α₁ связанного с заместителем атома углерода. Этот вопрос обсуждается в следующем разделе при рассмотрении I_π-эффекта.

Важно понимать, что донорная способность заместителей зависит от значений α₇ и β_1-7. Если α₇ велико и отрицательно, то электронная пара заместителя останется на нем. Кроме того, если β_1-7 очень мало, то это будет препятствовать переходу электронов в кольцо. Этот эффект экспериментально проявляется в том, что в N,N-диметил-орто-толуицие орто-пара-положения значительно менее активны, чем в N,N-диметиланилине.

Если N,N-диметильная группа образует с плоскостью бензольного кольца угол θ, то β_1-7 пропорционально cos θ: такой поворот называется стерическим отталкиванием метильной группы. На рис. 16.3 показано влияние изменения величин α₇ и β_1-7 на распределение хюккелевских зарядов в молекулах такого типа.

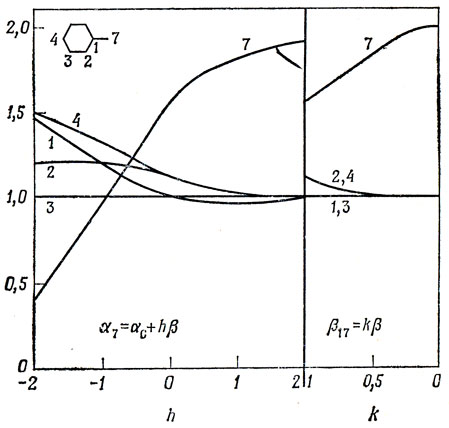
Рис. 16.3. Изменение плотностей заряда в бензильном анионе как функция хюккелевских параметров

Стирол и 2-фенильный анион также дают типичные примеры электроноакцепторных групп, например RC = 0, NO₂. Здесь имеется большее число гетеропараметров, но общее рассмотрение относительных акцепторных способностей проводится на основе тех же соображений, что и для донорных заместителей. Все акцепторные группы содержат атомы с большой электроотрицательностью, и это оправдывает их трактовку на основе модели бензильного катиона, рассмотренного выше. Например, в случае нитрогрупп получаем следующее вековое уравнение:

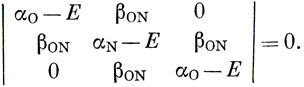
Если α_O очень мало по сравнению с α_N, имеем две МО, локализованные в основном на атомах кислорода и заполненные четырьмя π-электронами группы, и одну вакантную орбиталь, локализованную главным образом на атоме азота. Поскольку только энергия, соответствующая вакантной орбитали, близка к энергии МО бензольного кольца, взаимодействие нитрогруппы с кольцом лучше представлять моделью возмущенного бензильного катиона, а не возмущенного 2-фенилпропенила. Подобные соображения оправдывают использование модели бензильного катиона в трактовке карбонильной группы.