Глава 17. Химические реакции и относительная реакционная способность в органической химии

В этой книге рассматривается теория валентности, а не кинетика химических реакций. Тем не менее уместно задать вопрос: может ли теория валентности пролить некоторый свет на проблему относительных скоростей реакций?

Рассмотрим простейшую химическую реакцию Н + Н₂ → Н₂ + Н. Если атом водорода приближается к молекуле водорода, то электронная потенциальная энергия системы возрастает (так как молекула Н₃ нестабильна). Вычисления показывают, что для системы Н₃ минимуму энергии отвечает линейное расположение атомов ^*); это означает, что легче всего реакция идет в том случае, если три атома остаются на одной прямой. Изменение потенциальной энергии в ходе реакции показано качественно на рис. 17.1. Области максимума потенциальной энергии соответствует так называемое переходное состояние молекулы, а разность энергий в переходном и начальном состояниях известна как энергия активации.

^*) (Расчеты, проведенные в работе [25], наряду с другими вычислениями позволяют допускать, что на вершине кривой потенциальной энергии, возможно, имеется небольшое углубление.)

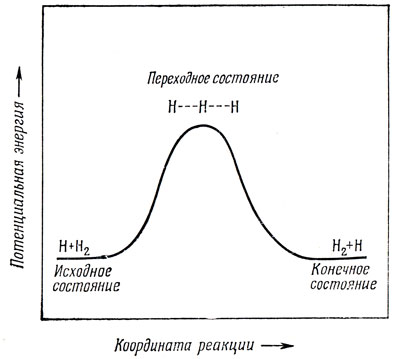
Рис. 17.1. Диаграмма потенциальной энергии для реакции H + H₂

Даже для этой простейшей из всех химических реакций результаты неэмпирического расчета поверхности потенциальной энергии находятся в умеренном согласии с экспериментом [5], и потому в случае более сложных реакций нужно обращаться к эмпирическим методам. Однако скорость химической реакции зависит от разности свободных энергий исходных молекул и переходного состояния, а не от энергии активации. Это вызвано тем, что эксперимент производят не с изолированными молекулами, а с совокупностью молекул с различными колебательными, вращательными и трансляционными энергиями. Таким образом, для расчета скорости химических реакций нужно пользоваться методами статистической механики, рассмотрение которых выходит за рамки этой книги. Результаты применения статистической теории скоростей реакций заключаются в следующем. Константу скорости реакции можно выразить через два параметра - ΔS^* (энтропия активации) и ΔH^* (энтальпия активации) - следующим образом:

Энтальпия активации ΔH^* непосредственно связана с разностью потенциальной энергии начального и переходного состояний, и, вероятно, можно оценить эту величину ΔH^*, используя теорию валентности.

В растворе сольватация реагирующих молекул и активированного комплекса вносит существенный вклад в ΔH^* и ΔS^*, и потому в настоящее время точный расчет этих величин практически невозможен. Для большинства реакций с участием органических молекул мы вынуждены ограничиться сравнением скоростей реакций, т. е. данных о свободной энергии, с расчетами изолированных молекул или молекулярных комплексов, т. е. с результатами, относящимися к идеализированной потенциальной энергии. Оправданием такого подхода служит следующее соображение: если сравнивать между собой реакции для ряда сходных соединений (например, нитрование ароматических углеводородов) при одних и тех же концентрациях и температуре, то разумно считать, что энтропийные и сольватационные факторы остаются постоянными в пределах ряда или изменяются по крайней мере определенным образом.

Наиболее широко такой подход применялся для описания реакции ароматического замещения. Довольно простую схему расчетов можно предложить на основе приближения Хюккеля. В следующем разделе рассматриваются некоторые пути осуществления таких расчетов.