17.2. Приближение изолированной молекулы

Существуют убедительные доказательства того, что при нитровании ароматической молекулы в концентрированной серной кислоте электрофильным реагентом является ион нитрония NO₂⁺. Поэтому можно предполагать, что существует связь между относительными скоростями нитрования в различных положениях молекулы и π-электронными зарядами в этих положениях. Такая связь обнаружена в случае, когда различия между π-зарядами велики. К сожалению, эти большие различия имеют место только тогда, когда участвующий в реакции углеводород содержит гетероатомы и, следовательно, вычисляемые электронные заряды зависят от выбора хюккелевских параметров для этих атомов. А так как все же остается некоторая неопределенность в значениях этих параметров, трудно получить убедительное подтверждение корреляции между π-зарядом и реакционной способностью. Качественно, однако, можно заключить, что (+К)-группы, отдающие электроны в ароматическое кольцо, направляют атаку реагентов в пара- и орто-положения кольца, а (-К)-группы - в мета-положение и с меньшей, чем для незамещенных молекул, скоростью.

Могут быть такие реакции электрофильного замещения, в которых атакующим реагентом не является положительный ион, и в таких случаях совсем не обязательно существование корреляции между скоростью реакции и электронной плотностью. Кроме того, в случае полициклических ароматических углеводородов распределение электронного заряда, вообще, не дает возможности судить о месте реакции замещения, потому что, как уже говорилось, в альтернантных углеводородах π-электронный заряд на любом из атомов, участвующих в сопряжении, равен единице. В неальтернантных углеводородах вычисляемые разности зарядов на различных атомах малы. По-видимому, для таких молекул более важным фактором является поляризация заряда, вызываемая атакующим реагентом.

Если заряженный реагент очень близко подходит к атому μ, то электронная плотность в этом месте изменяется. Если предположить, что атакующая группа изменяет величину кулоновского интеграла α_μ, то изменение электронного заряда можно выразить через самополяризуемость [см. выражение (15.33)]:

δα_μ, вероятно, будет велико лишь в том случае, когда атакующий реагент имеет высокую полярность (например, NO₂⁺), и потому только в этом случае можно ожидать существования корреляции между скоростью реакции и индексом π_{μ, μ}. Как видно из дальнейшего рассмотрения (табл. 17.1), корреляция проявляется довольно отчетливо. Поскольку наведенные заряды 6s обычно малы, δq_μ не будет надежной характеристикой реакционной способности, если уже имелись собственные заряды на атомах. По этой причине эта величина не играет существенной роли в теории реакционной способности гетерозамещенных молекул. Фукуи [27] предположил, что при определении направления электрофильной атаки существенны электронные заряды только для высшей связывающей МО, а при нуклеофильной атаке - для низшей разрыхляющей МО. Эти орбитали он назвал граничными орбиталями. В качестве простого примера рассмотрим электрон на высшей занятой МО бутадиена; ψ₂ вносит по 36% электронного заряда на атомы 1 и 4 и по 14% - на атомы 2 и 3 (см. стр. 351). Поэтому, согласно теории граничных орбиталей, электрофил будет атаковать предпочтительнее концевые атомы. А так как электронный заряд низшей разрыхляющей МО распределяется между атомами таким же образом, атака нуклеофильным реагентом будет происходить также в направлении концевых атомов.

Не существует прямого теоретического обоснования предположения Фукуи; такое обоснование можно получить косвенным путем, рассматривая соотношение между электронной плотностью граничных орбиталей и индексом сверхделокализуемости, введенным также Фукуи [28].

Электрофильный реагент имеет вакантную орбиталь с низкой энергией. Если эта орбиталь перекрывается с π-орбиталями углеводорода, то будет иметь место стабилизация переходного состояния вследствие делокализации электронов. Энергию делокализации можно вычислить во втором порядке теории возмущений. Пусть Е_s - энергия, соответствующая орбитали ψ_s электрофильного реагента, а Е_r - энергия связывающей орбитали ψ_r углеводорода; рассмотрим только случай, когда Е_s > Е_r. Если β' - резонансный интеграл, вычисленный с орбиталью замещающей группы и АО атакуемого атома углерода, то взаимодействие ψ_s- и ψ_r-орбиталей понижает энергию орбитали ψ_r на величину [см. выражение (6.54)]

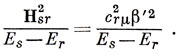
Полное понижение энергии получим, просуммировав по всем связывающим орбиталям и вводя множитель 2, потому что на каждой орбитали находятся два электрона:

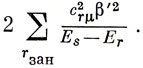
Это выражение имеет очевидное сходство с введенным Фукуи индексом сверхделокализуемости, который определен следующим образом:

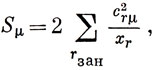
где х_r - безразмерный энергетический параметр Хюккеля, определенный по уравнению (15.4). Чем больше S_μ, тем больше величина энергии делокализации и тем меньше величина энергии активации.

Наиболее важный член в сумме (17.5) обусловлен в общем случае граничной орбиталью ψ₁, так как ей соответствует наименьшее значение х_r. Поэтому можно считать, что приближение сверхделокализуемости (не всегда хорошее) дается величиной

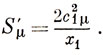
Однако с_1μ² характеризует электронную плотность граничной орбитали, и потому, если существует корреляция между скоростью реакции и S_μ', должна наблюдаться корреляция и между скоростью реакции и с_1μ². Это служит некоторым оправданием предположения Фукуи о важной роли граничной плотности.

Для объяснения корреляции между скоростью реакции и распределением электронного заряда были предложены модели, учитывающие перенос электронного заряда. В этих моделях полагают, что в промежуточном состоянии электрон переходит от углеводорода к электрофильному реагенту. Чем меньшая энергия требуется для такого перехода, тем легче идет реакция. Изложим кратко трактовку такой модели, проведенную Броуном, и покажем, что она также приводит к оправданию подхода, основанного на понятии граничных орбиталей.

Рассмотрим два состояния системы, состоящей из углеводорода и электрофильного реагента, отличающиеся местоположением положительного заряда. Для каждого из этих состояний можно построить диаграмму потенциальной энергии, как это показано на рис. 17.3. В силу взаимодействия между двумя состояниями и в соответствии с правилом непересечения (стр. 215) ход кривых потенциальной энергии в действительности будет тем, который представлен пунктирными линиями ^*).

^*) (Взаимодействие такого типа обсуждается более подробно в разд. 18.2.)

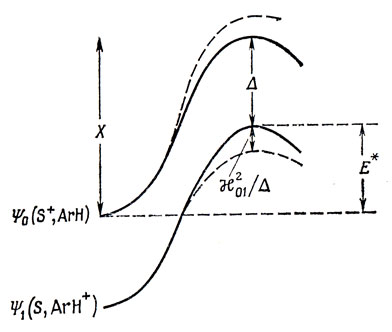
Рис. 17.3. Диаграмма потенциальной энергии для электрофильного замещения в модели с переносом заряда

Реагенты приближаются друг к другу таким образом, что потенциальная энергия изменяется в соответствии с верхней кривой. Но когда они сближаются, появляется возможность перехода с верхней кривой на нижнюю, с передачей электрона от углеводорода электрофильному реагенту.

Пусть Ψ₀ и Ψ₁ - волновые функции, соответствующие верхней и нижней кривым, как показано на рис. 17.3, и Δ - разность энергий в переходном состоянии до взаимодействия. Пусть X - величина энергии состояния Ψ₀, отсчитанная от энергии реагентов, H₀₁ - матричный элемент энергии, вычисленный с функциями Ψ₀ и Ψ₁ в переходном состоянии. Тогда энергия активации, рассчитанная на основе соотношения (6.54), равна

Величина Δ определяется разностью между сродством к электрону электрофильного реагента и потенциалом ионизации углеводорода. Последний равен, в приближении Хюккеля, βx₁; следовательно, имеем

где x_s - постоянная, характеризующая электрофильный реагент. Матричный элемент H₀₁ пропорционален хюккелевскому коэффициенту в граничной орбитали при АО атакуемого атома. Это записывается следующим образом:

Множитель √2 происходит от суммирования по спинам волновой функции Ψ₁ [см. выражение (9.24)]. Резонансный интеграл, вычисленный с акцепторной орбиталью электрофильного реагента и π-АО в месте атаки, равен gβ. Подставляя выражения (17.8) и (17.9) в соотношение (17.7), получим

Некоторый вклад в E^≠ вносит энергия сольватации, однако можно предполагать, что в сходных реакциях как эта энергия, так и величина X сохраняются. Поэтому Броун [7] вводит индекс реакционной способности следующим образом:

Параметр g характеризует взаимодействие в переходном состоянии: как g, так и х_s полагают постоянными параметрами во всех реакциях данного типа. Например, для реакции нитрования Броун принимал x_s = 2 и g = 0,6 и получил удовлетворительную корреляцию со скоростью реакции. В данном углеводороде для различных положений величина Z_μ зависит только от граничной плотности c_1μ², что служит еще одним доказательством в пользу метода граничных орбиталей.

Наконец, нужно упомянуть свободную валентность F_μ, определенную в выражении (15.13). В настоящее время этот индекс считают более сомнительным, нежели другие, описанные здесь.