17.3. Приближение локализации

B приближении локализации делается допущение, что чем ниже энергия σ-комплекса, тем ниже энергия переходного состояния. Это приближение учитывает изменение π-электронной энергии при образовании σ-комплекса (по отношению к энергии исходного углеводорода). Пусть хюккелевская энергия углеводорода до атаки электрофильным реагентом равна аα + bβ, а энергия σ-комплекса составляет (а - 2) α + b_μ⁺β (при образовании σ-комплекса число π-электронов уменьшается на два, так как два электрона участвуют в образовании связи с электрофильным реагентом). Тогда энергия локализации определяется разностью

Она составляет лишь ту часть полной энергии локализации, которая изменяется при изменении направления атаки.

Вычисление энергий локализации сводится к вычислению полной энергии углеводорода в приближении Хюккеля и полных хюккелевских энергий для фрагмента, получающегося при удалении из сопряженной системы одного атома углерода и двух π-электронов. Например, хюккелевская энергия молекулы бензола равна 6α + 8,00β; локализация двух электронов на одном из атомов приводит к возникновению пентадиенильного катиона, хюккелевская энергия которого равна 4α + 5,46β. Таким образом, для бензола L_μ⁺ β составляет 2,54β. Если в молекуле атомы углерода не равноценны, то и энергии локализации различны. Чем ниже энергия локализации, тем легче идет реакция при атаке в данное положение. Например, для молекулы азулена энергии локализации атомов таковы:

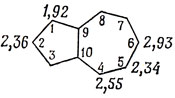
Поэтому можно полагать, что электрофильное замещение наиболее вероятно у атома 1, и этот вывод находится в полном согласии с экспериментом.

Дьюар показал, что для альтернантных углеводородов приближенные значения энергий локализации можно легко получить, зная орбитальные коэффициенты несвязывающей МО. Если имеется альтернантный углеводород RS с четным числом атомов углерода, то его можно представить себе состоящим из двух фрагментов R и S, которые являются нечетными альтернантными углеводородами. Например, бензол можно мысленно разбить либо на пентадиенильный фрагмент и атом углерода, либо на два аллильных фрагмента. Хюккелевская энергия молекулы RS связана с суммой энергий фрагментов R и S следующим приближенным соотношением:

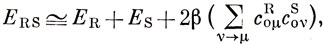
где c_oμ^R и c_oν^S - коэффициенты несвязывающих орбиталей фрагментов R и S соответственно для атомов с номерами μ (фрагмент R) и ν (фрагмент S), связанных между собой в исходной молекуле. Суммирование проводится по всем связям μ - ν.

Например, хюккелевская энергия аллильного радикала равна 3α + 2,83β, а коэффициенты помеченного набора в несвязывающих орбиталях равны ± 1/√2 (см. стр. 404). Таким образом, если бензол представлен в виде двух аллильных фрагментов

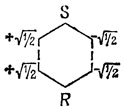
из выражения (17.13) получим

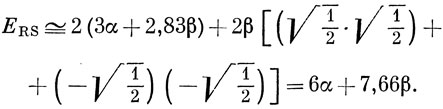
Эта величина близка к значению 6α + 8β, которое получается при обычном расчете бензола по методу Хюккеля.

Выражение (17.13) можно вывести следующим образом. Типичные примеры орбиталей фрагментов R и S показаны на рис. 17.4. Взаимодействие заполненных орбиталей не приводит к понижению энергии системы (см. задачу 15.6). Уменьшение энергии обусловлено взаимодействием несвязывающей и разрыхляющей орбиталей одного фрагмента с несвязывающей и связывающей орбиталями другого. Наиболее важным является взаимодействие между двумя несвязывающими орбиталями, которое приводит к возникновению двух МО молекулы

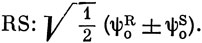
Понижение энергии низшей из этих двух МО относительно энергии несвязывающей МО дается выражением

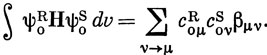
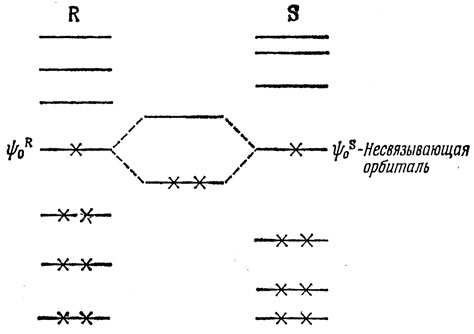
Рис. 17.4. Взаимодействие между орбиталями двух нечетных альтернантных углеводородов

Выражение (17.13) справедливо также для взаимодействия фрагментов R^- и S⁺ (или R⁺ и S^-), потому что и в этом случае на связывающей орбитали молекулы RS имеются два электрона, которые при разделении молекулы на фрагменты занимают несвязывающие орбитали каждого из них. При таком рассмотрении энергия системы RS всегда недооценивается по причине пренебрежения всеми взаимодействиями, кроме взаимодействия между двумя несвязывающими орбиталями.

Метод Дьюара применяется в основном для вычисления приближенных значений энергии локализации в результате замещения. Рассмотрим эти вычисления на частном примере, когда фрагмент S состоит из одного атома, у которого происходит замещение, тогда c_oν^S = 1, а с атомом ν связаны атомы μ и μ'. Из соотношения (17.13) находим

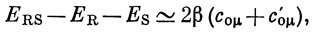
где с_0μ и c_0μ' - коэффициенты несвязывающей орбитали, относящиеся к соседям атома S. Величину 2 (c_oμ + c_oμ') называют индексом Дьюара и обозначают N_μ. Чем меньше индекс Дьюара, тем меньше энергия взаимодействия между фрагментами R и S и, следовательно, тем легче изолировать атом углерода от сопряженной системы.

Например, атака молекулы нафталина может приводить к возникновению одного из двух показанных ниже σ-комплексов.

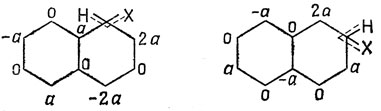
Коэффициенты несвязывающих орбиталей для обоих π-электронных фрагментов вычисляются по описанному ранее (стр. 406) методу и оказываются равными: а = 1/√11; N₁ = 6/√11 = 1,81 (для первого комплекса) и а = 1/√8; N₂ = 6/√8 = 2,12 (для второго комплекса). В первом положении величина N меньше, чем во втором, и потому замещение будет происходить чаще в первом положении; это находится в согласии с экспериментальными данными. Метод Дьюара нельзя применять к неальтернантным молекулам, потому что их фрагменты вообще не имеют несвязывающих орбиталей.