18.2. Донорно-акцепторные комплексы

Молекулярным комплексом называют группу из двух или большего числа молекул, связанных между собой. Типичные примеры таких комплексов: BF₃ ← NH₃ и хинон - гидрохинон (хингидрон). Оба эти комплекса можно приготовить в виде кристаллов с точно определенной стехиометрией 1:1. Известно также много примеров, когда объединение двух молекул в комплекс происходит в растворе (получить такие соединения в виде кристаллов не удается). Одним из примеров такого рода является комплекс иод-бензол.

Все эти комплексы имеют общую особенность: одна из молекул является донором электронов, а другая - акцептором:

Донором электронов является молекула, облагающая слабо связанными электронами (например, неподеленная пара в NH₃) и соответственно малым потенциалом ионизации. Благодаря этому свойству молекула может быть восстановителем или льюисовским основанием. Акцептор, с другой стороны, имеет вакантную орбиталь с низкой энергией (например, вакантная 2р-орбиталь в BF₃). Акцепторы обладают большим сродством к электрону и могут быть окислителями или льюисовскими кислотами. Однако на самом деле способность к захвату или отдаче электронов (акцепторное и донорное свойства) следует всегда рассматривать по отношению к партнеру в комплексе. Так, фенильная группа захватывает электроны заместителя в молекуле анилина, но отдает их заместителю в нитробензоле; точно так же бензол ведет себя как донор по отношению к молекуле иода, но как акцептор по отношению к молекуле или атому с более сильными донорными свойствами (например, щелочному металлу).

Во многих случаях донорно-акцепторный комплекс сильно окрашен. Например, гидрохинон бесцветен, а хинон желтого цвета: кристаллы же хингидрона имеют характерный зеленый цвет с металлическим отливом. Аналогично растворы бензол - иод обнаруживают в ультрафиолетовой области полосу поглощения около 3000 А, которая отсутствует в спектрах иода и бензола в отдельности.

Первое удовлетворительное квантовомеханическое рассмотрение таких молекулярных комплексов было проведено Малликеном. Он показал, что как стабильность комплексов, так и их характерные электронные спектры поглощения связаны с донорно-акцепторными свойствами.

Пусть Ψ(D) и Ψ(А) - соответственно волновые функции донора и акцептора в отдельности. Волновую функцию системы из невзаимодействующих донора и акцептора можно записать в виде

Подобно этому, если имеются ионы D⁺ и А^-, разведенные на большое расстояние, волновой функцией такой системы является

Когда две молекулы сближаются и их электронные облака перекрываются, то обе волновые функции следует исправить таким образом, чтобы учесть возможность обмена электронов в соответствии с принципом антисимметрии. Формально это можно сделать, если ввести оператор антисимметризации, который преобразует простое произведение в антисимметризованную сумму произведений ^*).

^*) (А φ_а (1) φ_b (2) = √1/2 {φ_а (1) φ_b (2) - φ_а (2) φ_b (1)} - простейший пример антисимметризации. Однако D и А могут не описываться волновыми функциями, состоящими из одного произведения спин-орбиталей, и антисимметризатор A не обязательно преобразует исходную функцию в слэтеровский определитель.)

Запишем полную волновую функцию молекулярного комплекса в виде линейной комбинации этих двух функций

и определим коэффициенты этой комбинации, решая соответствующие уравнения. При этом получим два решения. Соответствующие волновые функции можно представить в виде

Энергия, соответствующая функции Ψ₀, ниже энергий, отвечающих функциям Ψ (D, А) и Ψ (D⁺, - А^-) в отдельности, и потому возможное объяснение стабильности комплекса следует искать именно во взаимодействии этих состояний. Электронный переход Ψ₀ → Ψ₁, которому нет аналога ни у донора, ни у акцептора, можно связать с полосами поглощения, характерными для комплекса.

Рассмотрим сначала слабые комплексы, которые обычно образуются органическими молекулами. В этом случае состоянию Ψ (D, А), которое Малликен называет несвязывающим, соответствует значительно более низкая энергия, чем ионному (с переносом заряда) состоянию Ψ (D⁺, - А^-). Кроме того, матричный элемент гамильтониана, вычисленный с функциями Ψ (D, А) и Ψ (D⁺, - А^-), обычно мал. Поэтому волновую функцию основного состояния можно записать в виде

где b₀ << 1, а волновую функцию возбужденного состояния в виде

где а₁ << 1. Поэтому электронный переход Ψ₀ → Ψ₁ сопровождается переносом почти целого заряда электрона от донора к акцептору, а полосу поглощения, связанную с таким переходом, называют полосой, обусловленной переносом заряда.

Наиболее сильным аргументом в пользу такой интерпретации полосы поглощения является частота перехода. Если взаимодействие между двумя компонентами волновой функции мало, то энергия перехода Ψ₀ → Ψ₁ почти совпадает с энергией перехода

т. е. приближенно равна [см. выражение (11.34)]

Для ряда комплексов с одним и тем же акцептором, но различными донорами, соотношение

где К - постоянная, выполняется удивительно хорошо, как видно из рис. 18.1. Это означает, что, хотя кулоновская энергия Q взаимодействия двух ионов довольно велика, она не сильно зависит от природы донора.

Рис. 18.1. Корреляция между энергией в максимуме полосы, обусловленной переносом заряда, и потенциалом ионизации донора для комплексов иода с органическими донорами [6]

Взаимодействие между несвязывающим и возникшим в результате переноса заряда состояниями зависит от перекрывания теряющей электрон орбитали донора D (донорной орбитали) с орбиталью акцептора А (акцепторной орбиталью), которая захватывает электрон. Это легко видеть в простейшем случае одноэлектронной системы:

где ψ_d - донорная орбиталь D; ψ_a - акцепторная орбиталь А. Тогда

и этот интеграл обращается в нуль, когда орбитали ψ_d и ψ_а не перекрываются: если в любой точке некоторой области или ψ_d или ψ_a равны нулю, то вклад в интеграл по этой области пространства равен нулю. В общем случае интеграл взаимодействия приблизительно пропорционален интегралу перекрывания S_da, a энергия стабилизации пропорциональна S_dа² (второй порядок взаимодействия) [см. выражение (17.7)].

В типичных органических комплексах, подобных хингидрону, донорные и акцепторные орбитали представляют собой делокализованные молекулярные π-МО и область перекрывания этих двух орбиталей делокализована, как это показано на рис. 18.2. Если говорят о химической связи между двумя компонентами молекулярного комплекса, нужно помнить, что эта связь - делокализованная, и ее невозможно изобразить, рисуя линию, соединяющую два атома. Энергия связи комплексов типа хингидрона обычно лежит в интервале 0,1-0,5 эв (2-10 ккал/моль). Это немного больше, чем энергии, которые соответствуют лондоновским дисперсионным силам взаимодействия, и потому, хотя получены убедительные доказательства, позволяющие объяснять образование комплексов в таких случаях переносом заряда, довольно большая часть энергии связи происходит, вероятно, от дисперсионных сил.

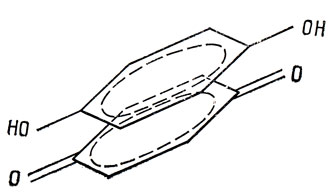
Рис. 18.2. Структура хингидрона

К совершенно другому случаю относятся комплексы типа BF₃ ← NH₃. Расчет показывает, что в этих комплексах состоянию Ψ (D⁺, А^-) соответствует приблизительно та же энергия, что и состоянию Ψ (D, А), и одно лишь это говорит в пользу большой энергии связи. Но, что более важно, донорные и акцепторные орбитали теперь не являются делокализованными МО, а представляют собой сильно перекрывающиеся гибридные АО. Взаимодействие между несвязывающим и возникшим при переносе заряда состояниями дает для энергии связи комплекса BF₃ ← NH₃ величину около 2 эв, что много больше энергии связи для комплексов типа хингидрона. Эта большая стабилизация основного состояния должна сопровождаться большой дестабилизацией (повышением энергии) возбужденного состояния. В случае комплекса BF₃ ← NH₃ расстояние между уровнями энергии основного и возбужденного состояний слишком велико для того, чтобы полоса, соответствующая переходу с переносом заряда, наблюдалась в области более длинноволновой, чем 2300 А, где начинается собственное поглощение NH₃.

Теория переноса заряда в молекулярных комплексах, рассмотренная здесь, очень похожа на метод ВС в применении к двухатомным молекулам. Это становится совершенно очевидным, если в качестве D и А взять атомы, а не молекулы. Как уже говорилось, простейшая волновая функция, построенная по методу ВС, лучше, чем простейшая функция метода МО, если атомы слабо связаны друг с другом, так как в предельном переходе МО приводит к неверному описанию продуктов диссоциации. Поэтому теория переноса заряда в слабых молекулярных комплексах дает лучшее описание, чем трактовка по методу МО, в которой электроны размещают на орбиталях, делокализованных в области донора и акцептора. С другой стороны, для комплексов с сильной связью, где основное состояние может быть представлено почти равной смесью функций Ψ (D, А) и Ψ (D⁺, А^-), столь же хорошо и, возможно, даже лучше использовать делокализованные МО. В методе МО нет различия между связью В - N в BF₃ ← NH₃ и связью Li - Н: обе двухэлектронные связи имеют в большой степени ионный характер.

Термин "перенос заряда", используемый при описании связи в молекулярном комплексе, понимается в том же смысле, как и термины "структура" и "резонанс". Эти понятия связаны с частной квантовомеханической моделью, а не с физически наблюдаемыми величинами. С другой стороны, когда термин "перенос заряда" используется в описании электронной полосы поглощения, то имеется в виду, что при возбуждении комплекса значительная часть электронного заряда передается от донора к акцептору, и с этой точки зрения перенос заряда означает не просто условное понятие, а нечто значительно более реальное.