Глава 9

9.1. Для доказательства достаточно непосредственно продифференцировать произведение, например

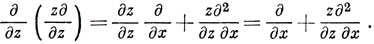
9.2. Примените правило, приведенное на стр. 157.

9.3. Установите возможные значения спина двух электронов, а затем определите, какие значения спина возникают при добавлении спина третьего электрона.

9.4. Выполните ту же самую процедуру, которая была использована при построении табл. 9.3, а затем учтите взаимно однозначное соответствие между значениями M_L, M_S для обеих конфигураций.

9.5. Единственной, еще не рассмотренной конфигурацией является р³. Она дает термы ⁴S, ²Р и ²D.

9.6. Вычислите разность энергий уровней с квантовыми числами J, L, S и J - 1, L, S.

9.7. См. стр. 162.

9.8. Для конфигурации 3p3d имеет место связь L - S, для конфигурации 3р6d - связь j - j. Убедитесь, что в обоих случаях имеет место взаимно однозначное соответствие в значениях J.

9.9. Начните с волновой функции терма ¹D, для которого L = 2, M_L = 2. Она соответствует двум электронам с противоположными спинами на р-орбитали с m = 1 (см. табл. 9.3). Напишите соответствующую этому случаю антисимметризованную функцию. Подействуйте на нее оператором L_- = L_- (1) + L_- (2) - оператором сдвига обоих электронов 1 и 2. Для того чтобы получить результат такой операции, воспользуйтесь формулой (9.21). Оператор L_-, действуя на компоненту с L = 2, M_L = 2, переводит ее в компоненту L = 2, M_L = 1. Вид этой функции получается из рассмотрения действия операторов L_- (1) и L_- (2) на p-орбитали.

9.10. Правила отбора для случая рассел-саундерсовой (L - S) связи приведены на стр. 169.

9.11. Слабое магнитное поле расщепляет уровень с квантовым числом J на 2J + 1. равноотстоящих уровня, расстояние между которыми определяется выражением (9.27).

9.12. Напишите 1s-орбиталь в виде 1s = 2ζ^3/2е^-ζr Y₀₀ (θ, φ) и затем проинтегрируйте по угловым координатам, что дает единицу. Интеграл по координатам первого электрона разбейте на два интеграла, как это описано на стр. 176.

9.13. Возьмите антисимметризованную функцию состояния ³S при M_S = 1. Возведите ее в квадрат и просуммируйте по спинам, чтобы получить Р (r₁, r₂). Тогда Р (r₁)= ∫ Р (r₁, r₂) dυ₂ и т. д., откуда можно получить требующееся выражение.