Глава 3

3.1. Рис. 19.3.

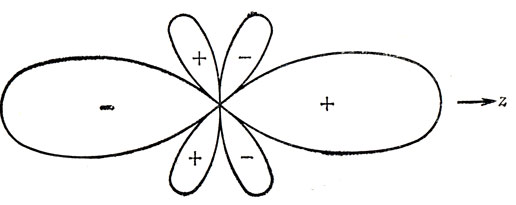
Рис. 19.3

3.2. р-Орбиталь с составляющими (1, 1, 1) должна содержать смесь орбиталей р_x, р_у и p_z с одинаковыми коэффициентами. После нормировки волновая функция примет вид Ψ (1, 1, 1) =

= √1/3 (p_x + p_y + p_z).

Другими словами, 1/√3 есть косинус угла, который вектор (1, 1, 1) образует с любой из осей координат.

3.3. Из табл.3.3 имеем

Вводя не зависящую от n постоянную σ = Zr/a₀, имеем

Требуется доказать, что

Докажем это, показав, что интегрирование по радиальной координате дает нуль. Переходя в интеграле от радиальной части к переменной σ, рассмотрим

Используя формулу, приведенную в указании к решению задачи 3.4, найдем, что этот интеграл равен

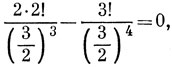
т. е. соотношение ортогональности действительно выполняется. 3.4.

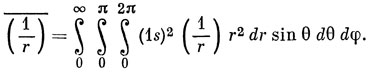
Из табл. 3.3 имеем

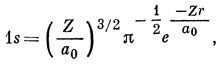
отсюда

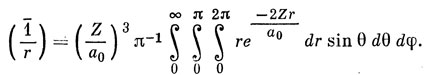
Далее, ∫₀^2π dφ = 2π, ∫₀^π sin θ dθ = 2, ∫₀^∞ r e^-2Zr/a₀ dr = (a₀/2Z)². Отсюда (1^-/r) = Z/a₀. Потенциальная энергия равна - Ze²/r, следовательно, среднее значение потенциальной энергии составляет - Z²e²/a₀. Поскольку полная энергия равна [см. выражение (3.19)] - Z²e²/2a₀, то средняя кинетическая энергия составляет Z²e²2/a₀, таким образом, выполнена теорема вириала Т^- = - Е.